Задача 61440 Вычислить объём тела, заданного...
Условие
используя его поперечные сечения
z=2+x^2+9y^2;z=4
895
Решение
★
[m]V=∫^{2}_{0}S(z)dz[/m]
Где [m]S(z) [/m]- площадь сечения плоскостями, параллельными плоскости хОу
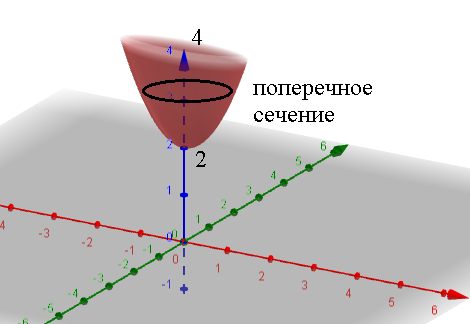
В сечениях получатся[b] эллипсы:[/b] ( см. рис.)
[m]z=2+x^2+9y^2[/m]
[m]x^2+9y^2=z-2[/m]
2 ≤ z ≤ 4
[m]\frac{x^2}{(z-2)}+\frac{y^2}{\frac{1}{9}(z-2)}=1[/m] ⇒
Площадь эллипса [m]\frac{x^2}{a^2}+\frac{y^2}{b^2}=1[/m] равна [m]πab[/m]
Поэтому
[m]S(z)=π\cdot \sqrt{(z-2)}\cdot \sqrt{\frac{1}{9(z-2)}}=\frac{π}{3}\cdot (z-2)[/m]
[m]V=∫^{4}_{2}\frac{π}{3}\cdot (z-2)dz=\frac{π}{3}\cdot \frac{(z-2)^2}{2}|^{4}_{2}=\frac{2π}{3}[/m]