Задача 614 Найдите площадь треугольника, если две...

slava191

13.02.2014

Найдите площадь треугольника, если две стороны его равны 27 и 29, а медиана, проведённая к третьей, равна 26.

Пусть стороны АВ и ВС треугольника ABC равны соответственно 27 и 29, а его медиана ВМ равна 26. На продолжении медианы ВМ за точку М отложим отрезок MD, равный ВМ. Из равенства треугольников АВМ и CDM следует равенство площадей треугольников ABC и BCD. В треугольнике BCD известно, что
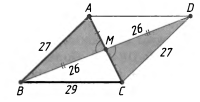
ВС = 29, BD = 2ВМ = 52, DC = АВ = 27.
По формуле Герона
S BCD = 270 = S ABC



Ответ: 270.