Задача 613 Медиана AM треугольника ABC равна m и...
Условие
математика 10-11 класс
11493
Решение
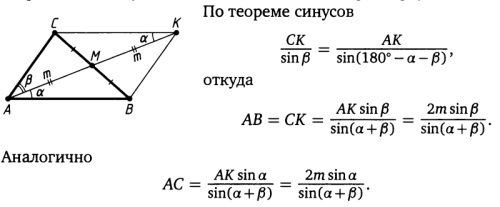
Ответ: В решение

Ответ: В решение