Задача 60866 Изобразите на координатной плоскости...
Условие
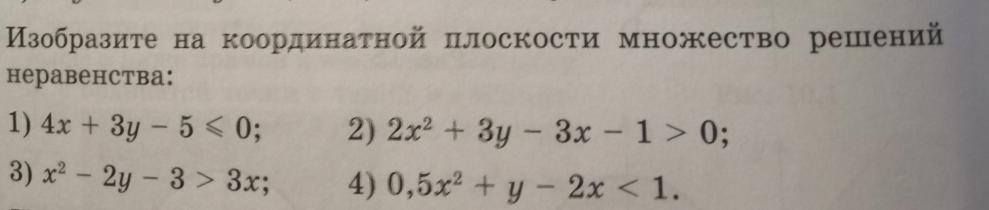
Решение
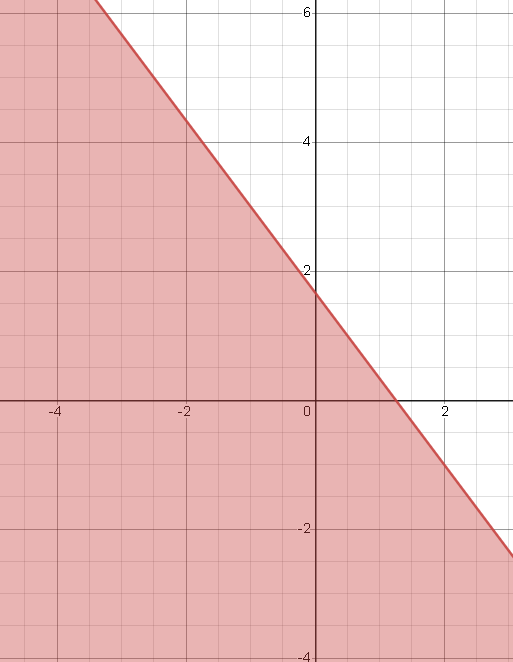
Пусть x=2; тогда 4*2+3у-5=0 ⇒ 3y=5-8; 3y=-3; y=-1
Пусть x=-1; тогда 4*(-1)+3у-5=0 ⇒ 3y=5+4; 3y=9; y=3
Строим по двум точкам.
(2;-1) и (-1;3)
Прямая разбивает плоскость на две части.
Берем произвольную точку.
Например (0;0)
Подставляем ее координаты в неравенство:
4*0+3*0-5 ≤ 0 - верно
Закрашиваем ту часть плоскости, которая содержит точку (0;0)
Неравенство нестрогое, граница области - сплошной линией
Если бы было строгое (> или <) неравенство, то границу изобразили бы пунктирной линией
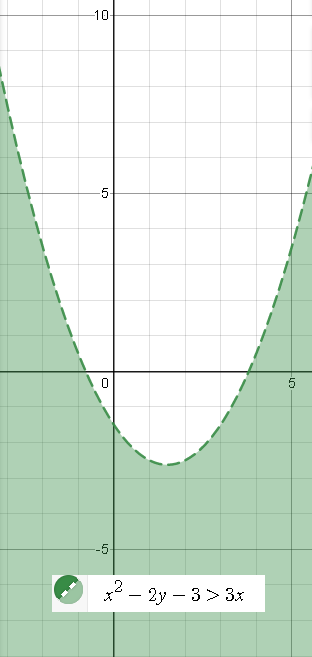
3)
граница области - парабола
x^2-2y-3=3x
⇒
y=(x^2-3x-3)/2
y=(1/2)x^2-(3/2)x-(3/2)
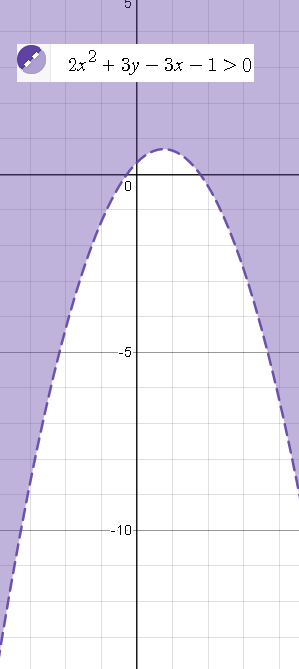
2)
граница области - парабола
2x^2+3y-3x-1=0
⇒
y=(-2x^2+3x+1)/3
y=-(2/3)x^2+x+(1/3)