Задача 60816 ...

614d568e7c1408291d404e66

24.09.2021 07:42:38

24 вариант

Задание №2

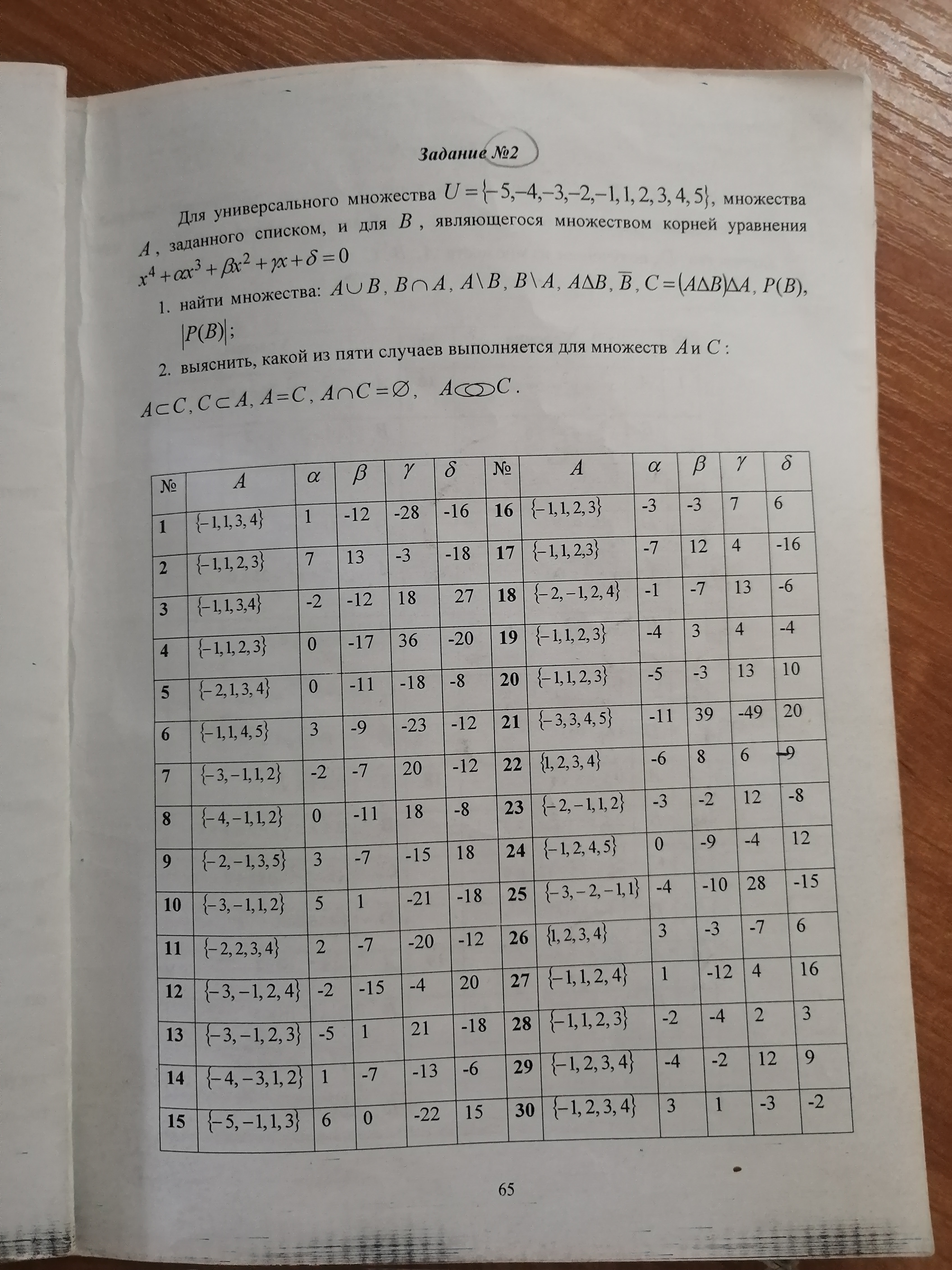
Для универсального множества U={-5,−4,−3,−2,−1,1,2,3,4,5], множества A, заданного списком, и для B, являющегося множеством корней уравнения x^4 + 3x^3 + βx^2 + γx + δ = 0

1. найти множества: A∪B, B∩A, A\B, B\A, A∆B, B ⊂ C=(A∆B)∪A, P(B),
P(B);

2. вычислить, какой из пяти случаев выполнится для множеств A и C:
Нет A∩C=Ф, A⊂C.

5f3ea7e3faf909182968ddd9

24.09.2021 12:09:21

★

A={-1;2;4;5}

B={-2;1;3} - множество корней уравнения x^4-9x^2-4x+12=0

Корни уравнения - делители свободного члена ( св. число 12)

± 1; ± 2; ± 3; ± 4; ± 6; ± 12

Проверкой убеждаемся, что корни: -2; 1; 3

Можно разложить многочлен x^4-9x^2-4x+12 на множители:


x^4-9x^2-4x+12=x^2(x^2-9)-4(x-3)=x^2*(x-3)*(x+3)-4(x-3)=(x-3)*(x^3+3x^2-4)=(x-3)*((x^3-1)+(3x^2-3))=

=(x-3)(x-1)*(x^2+x+1+3x+3)=(x-3)*(x-1)*(x+2)^2


A ∪ B={-1;2;4;5}U{-2;1;3} ={–2;–1;1;2;3;4;5}

A ∩ B ={-1;2;4;5} ∩ {-2;1;3} = ∅ ( нет общих элементов)

A \ B={-1;2;4;5}\{-2;1;3}={-1;2;4;5}

B \ A={-2;1;3}\{-1;2;4;5}={-2;1;3}


A Δ B=(A \ B) U (B \ A)={-1;2;4;5}U{-2;1;3}={–2;–1;1;2;3;4;5}

vector{B}=U\B={–5;–4;–3;-2;-1;1;2;3;4;5}\{-2;1;3}={–5;–4;–3;-1;2;4;5}


C =(A Δ B) ΔA=((A ΔB)\A) U (A\ (A Δ B))={-2;1;3}


(A ΔB)\A={–2;–1;1;2;3;4;5} \{-1;2;4;5}={-2;1;3}


A\ (A Δ B)={-1;2;4;5}\{–2;–1;1;2;3;4;5} = ∅

((A ΔB)\A) U (A\ (A Δ B))={-2;1;3}U ∅ ={-2;1;3}