Задача 60798 Прошу помочь...
Условие
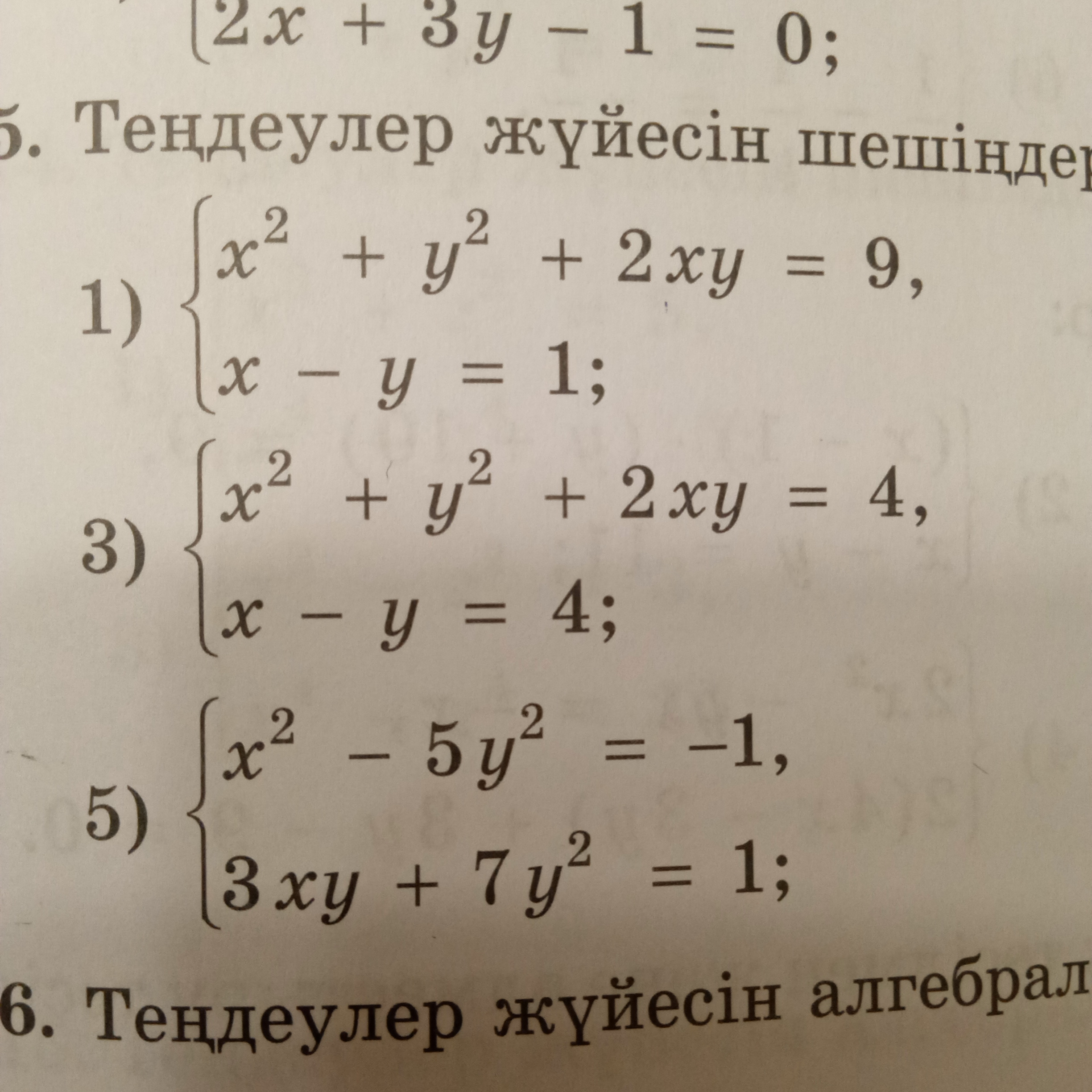
Решение
[m]\left\{\begin {matrix}x^2+y^2+2xy=9\\x-y=1\end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}x^2+y^2+2xy=9\\x=y+1\end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}(y+1)^2+y^2+2(y+1)y=9\\x=y+1\end {matrix}\right.[/m] ⇒
[m]\left\{\begin {matrix}y^2+2y+1+y^2+2y^2+2y=9\\x=y+1\end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}4y^2+4y-8=0\\x=y+1\end {matrix}\right.[/m] ⇒ [m]\left\{\begin {matrix}y^2+y-2=0\\x=y+1\end {matrix}\right.[/m]
y^2+y-2=0
D=1-4*(-2)=1+8=9
y_(1)=(-1-3)/2=-2; y_(2)=(-1+3)/2=1
[m]\left\{\begin {matrix}y_{1}=-2\\x_{1}=-2+1\end {matrix}\right.[/m]или [m]\left\{\begin {matrix}y_{2}=1\\x_{2}=1+1\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}y_{1}=-2\\x_{1}=-1\end {matrix}\right.[/m] или [m]\left\{\begin {matrix}y_{2}=1\\x_{2}=2\end {matrix}\right.[/m]
5)
Умножим второе уравнение на 2
[m]\left\{\begin {matrix}x^2-5y^2=-1\\ 6xy+14y^2=2\end {matrix}\right.[/m]
Складываем, т.е заменяем одно из уравнений системы на сумму уравнений:
[m]\left\{\begin {matrix}x^2-5y^2=-1\\ x^2+6xy+14y^2-5y^2=2-1\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}x^2-5y^2=-1\\ x^2+6xy+9y^2=1\end {matrix}\right.[/m]
Формула:
[m]\left\{\begin {matrix}x^2-5y^2=-1\\ (x+3y)^2=1\end {matrix}\right.[/m] ⇒ две системы
[m]\left\{\begin {matrix}x^2-5y^2=-1\\ x+3y=-1\end {matrix}\right.[/m] или [m]\left\{\begin {matrix}x^2-5y^2=-1\\ x+3y=1\end {matrix}\right.[/m]
Решаем системы способом подстановки:
[m]\left\{\begin {matrix}(-1-3y)^2-5y^2=-1\\ x=-1-3y\end {matrix}\right.[/m] или [m]\left\{\begin {matrix}(1-3y)^2-5y^2=-1\\ x=1-3y\end {matrix}\right.[/m]
Решайте...