Задача 60742 Используя признак Даламбера, исследовать...
Условие
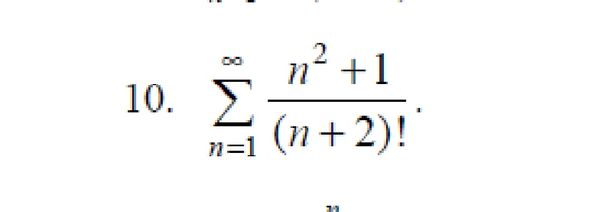
математика
311
Решение
★
[m]a_{n+1}=\frac{(n+1)^2+1}{((n+1)+2)!}=\frac{n^2+2n+1+1}{(n+1+2)!}=\frac{n^2+2n+2}{(n+3)!}[/m]
Применяем признак Даламбера:
[m] lim_{n → ∞ } \frac{a_{n+1}}{a_{n}}= lim_{n → ∞ }\frac{\frac{n^2+2n+2}{(n+3)!}}{\frac{n^2+1}{(n+2)!}}=[/m]
[m]= lim_{n → ∞ }\frac{n^2+2n+2}{(n+3)!}\cdot \frac{(n+2)!}{n^2+1}= lim_{n → ∞ }\frac{n^2+2n+2}{n^2+1}\cdot lim_{n → ∞ }\frac{(n+2)!}{(n+3)!}=1\cdot lim_{n → ∞ }\frac{1}{n+3}=1\cdot 0=0<1[/m]
Cходится