Задача 60528 ...
Условие
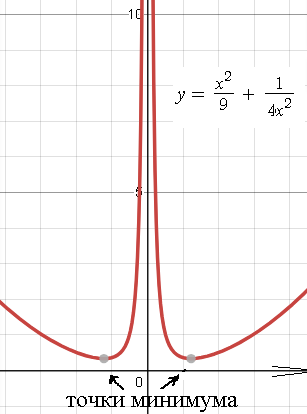
y = x^2/9 + 1/4x^2.
A) (3; +∞)
B) (0; +∞)
C) [1/6; +∞)
D) [1/36; +∞)
E) [1/3; +∞)
математика 10-11 класс
326
Решение
★
[m]y`=\frac{}{9}\cdot (x^2)`+\frac{1}{4}\cdot (x^{-2})`[/m]
[m]y`=\frac{2x}{9}-\frac{2}{4x^3}[/m]
[m]y`=0[/m] ⇒[m] \frac{2x}{9}-\frac{2}{4x^3}=0[/m] ⇒ [m] \frac{2x}{9}=\frac{2}{4x^3}[/m]
[m]8x^4=18[/m]
[m]x^2=3/2[/m]
⇒
x= ± sqrt(3/2) - точки экстремума функции, а именно точки минимума
Значение функции в этих точках
[m]y=\frac{}{9}\cdot (\frac{3}{2})+\frac{1}{4\cdot (\frac{3}{2}}=\frac{1}{6}+\frac{1}{6}=\frac{2}{6}=\frac{1}{3}[/m]
О т в е т. [m][\frac{1}{3};+ ∞ )[/m]