Задача 60200 Найти решение задачи Коши a) y' - y/x =...
Условие
a) y' - y/x = x sin x, y(pi/2) = 1
b) 3(xy' + y) = y^2 ln x, y(1) = 3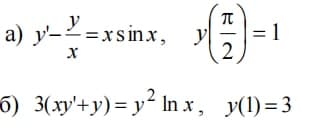
Решение
Решаем методом Бернулли
(введение двух функций):
y(x)=u(x)*v(x)
y`=u`*v+u*v`
Подставляем в уравнение:
u`*v+u*v`-(1/x)*u*v=xsinx
Группируем:
u`*v+(u*v`-(1/x)*u*v)=xsinx ⇒
u`*v+u*(v`-(1/x)*v)=xsinx
Полагаем
[blue]v`-(1/x)*v=0[/blue]
тогда
[blue]u`*v+u*0=xsinx [/blue]
Решаем два уравнения с разделяющимися переменными
1)[blue]v`-(1/x)*v=0[/blue]
dv/v=dx/x
∫ dv/v= ∫ dx/x
ln|v|=ln|x|
v=x
Подставляем во второе:
2)
u`*x+u*0=xsinx [/blue] ⇒
u`=sinx
u= ∫ sinxdx
u=-cosx+C
y=(-cosx+C)*x
[b]y=-xcosx+Cx[/b]- общее решение диф уравнения
y(π/2)=1 ⇒
[b]1=-(π/2)*cos(π/2)+C*(π/2)[/b] ⇒ C=(2/π)
[b]y=-xcosx+(2/π)*x[/b]- решение задачи Коши
2.
[m]3\cdot (xy`+y)=(lnx)\cdot y^2[/m]
Раскрываем скобки:
[m]3\cdot xy`+3\cdot y=(lnx)\cdot y^2[/m]
Делим на [m]3x[/m]
[m]y`+\frac{1}{x}\cdot y=\frac{lnx}{3x}\cdot y^2[/m] - уравнение Бернулли, n=2
Делим на [m]y^2[/m]:
[m]\frac{1}{y^2}y`+\frac{1}{x}\cdot \frac{1}{y}=\frac{lnx}{3x}[/m]
Подстановка : [m] z=\frac{1}{y}[/m] ⇒ [m] z`=-\frac{1}{y^2}\cdot y`[/m]
[m]-z`+\frac{1}{x}\cdot z=\frac{lnx}{3x}[/m] ⇒
[m]z`-\frac{1}{x}\cdot z=-\frac{lnx}{3x}[/m] - линейное уравнение первого порядка.
Решаем методом Бернулли:
Вводим в рассмотрение произведение [m]u(x)\cdot v(x)=z(x)[/m] ⇒ [m]z`=u`\cdot v+u\cdot v`[/m]
[m]u`\cdot v+u\cdot v`-\frac{1}{x}\cdot u\cdot v=-\frac{lnx}{3x}[/m]
Группируем:
[m]u`\cdot v+(u\cdot v`-\frac{1}{x}\cdot u\cdot v)=-\frac{lnx}{3x}[/m]
[m]u`\cdot v+u\cdot ( v`-\frac{1}{x}\cdot v)=-\frac{lnx}{3x}[/m]
Полагаем
[m]v`-\frac{1}{x}\cdot v=0[/m]
тогда
[m]u`\cdot v+u\cdot 0=-\frac{lnx}{3x}[/m]
Решаем два уравнения с[i] разделяющимися переменными[/i]:
[m]v`-\frac{1}{x}\cdot v=0[/m] ⇒ [m]\frac{dv}{dx}=\frac{1}{x}\cdot v[/m] ⇒ [m]\frac{dv}{v}=\frac{dx}{x}[/m]
Интегрируем:
[m] ∫ \frac{dv}{v}= ∫ \frac{dx}{x}[/m]
[m]ln|v|=ln|x|[/m] ⇒ [m]v=x[/m]
[m]u`\cdot x=-\frac{lnx}{3x}[/m] ⇒ [m]\frac{du}{dx}=-\frac{lnx}{3x^2}[/m] ⇒ [m]du=-\frac{lnx}{3x^2}dx[/m]
Интегрируем:
[m] ∫ du=- ∫ \frac{lnx}{3x^2}dx[/m]
Интегрируем по частям:
[m] u= \frac{1}{3}∫ (lnx)d(\frac{1}{x})[/m]
[m]u=- \frac{1}{3}\cdot (lnx)\cdot(-\frac{1}{x})-(-\frac{1}{3})\cdot ∫(-\frac{1}{x})\cdot \frac{1}{x}dx=\frac{lnx+1}{3x} +C [/m]
[m]z=u\cdot v=(\frac{lnx+1}{3x} +C)\cdot x[/m]
[m]z=\frac{lnx+1}{3} +C\cdot x[/m]
Обратная замена:
[m]y=\frac{1}{z}[/m] ⇒[m]y=\frac{3}{lnx+1+Cx}[/m]
Решение задачи Коши
y(1)=3
[m]3=\frac{3}{ln1+1+C}[/m] ⇒ [m]C=0[/m]
[m]y=\frac{3}{lnx+1}[/m]