Задача 60124 ...
Условие
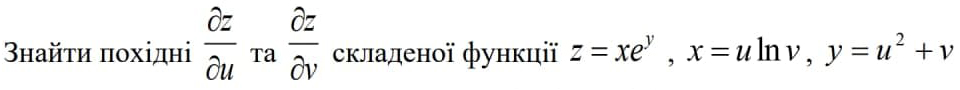
Решение
[m]\frac{ ∂z }{ ∂v}=\frac{ ∂z }{ ∂x}\cdot \frac{ ∂x }{ ∂v}+\frac{ ∂z }{ ∂y}\cdot \frac{ ∂y }{ ∂v}[/m]
Находим:
производная по переменной х, при этом y - постоянная
[m]\frac{ ∂z }{ ∂x}=(x\cdot e^{y})`_{x}=e^{y}[/m]
производная по переменной y, при этом x - постоянная
[m]\frac{ ∂z }{ ∂y}=(x\cdot e^{y})`_{y}=x\cdot e^{y}[/m]
производная по переменной u, при этом v - постоянная
[m] \frac{ ∂x }{ ∂u}=(u\cdot lnv)`_{u}=lnv[/m]
[m] \frac{ ∂y }{ ∂u}=(u^2+v)`_{u}=2u[/m]
производная по переменной v, при этом u - постоянная
[m] \frac{ ∂x }{ ∂v}=(u\cdot lnv)`_{u}=u\cdot \frac{1}{v}[/m]
[m] \frac{ ∂y }{ ∂v}=(u^2+v)`_{v}=1[/m]
Подставляем в первые две строчки.