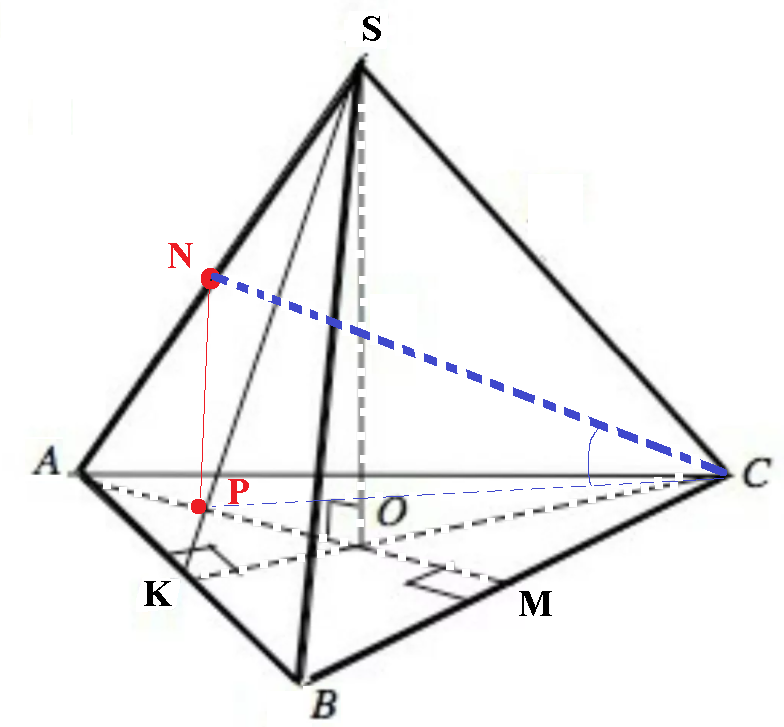
Задача 59890 В правильной треугольной пирамиде SABS с...

602a90393cfdeb46290c929b

24.05.2021 17:18:46

В правильной треугольной пирамиде SABS с основанием АВС известны рёбра: \}` = 2\/2. Найдите угол, образованный плоскостью основания и прямой С, где № — середина ребра AS Ответ: _

5f3ea7e3faf909182968ddd9

24.05.2021 20:46:01

★

AN=NS
P- проекция точки N

⇒

AP=PO

Из Δ АВС:
AM=AB*sin60 ° = sqrt(3)* sqrt(3)/2=3/2

AO=(2/3)AB=1 ( точка O- точка пересечения высот, [b]медиан [/b]и биссектрис)

Медианы в точке пересечения делятся в отношении 2:1, считая от вершины.


AP=0,5

SA=SC=SB=2sqrt(2)

⇒
AN=NS=sqrt(2)


Из ANP:

NP^2=AN^2-AP^2=(sqrt(2))^2-(0,5)^2=2-(1/2)=3/4

[b]NP=sqrt(3)/2[/b]


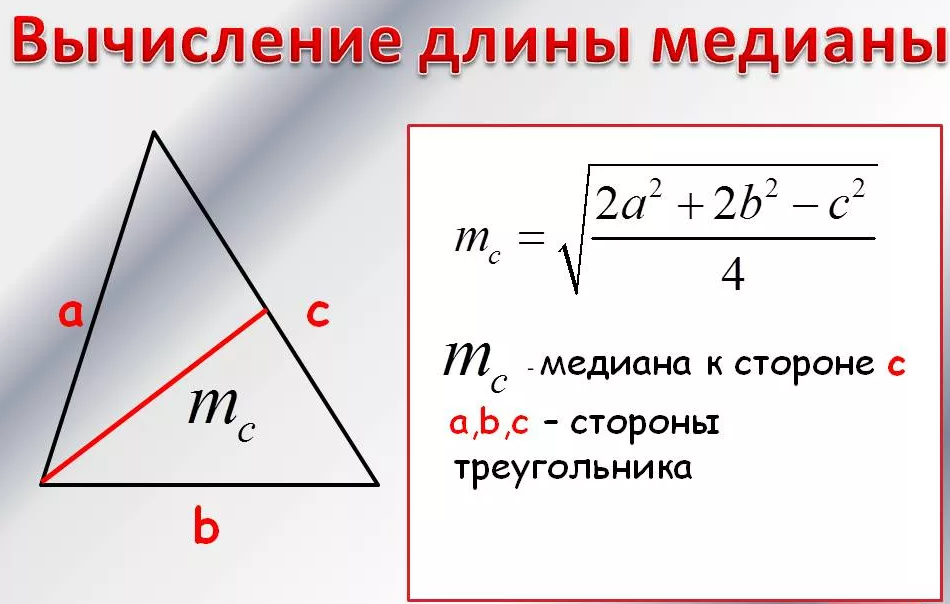
Из равнобедренного Δ ASC найдем CN

(CN- медиана)

Можно применить формулу ( см. скрин)


Из Δ С NP

sin ∠ NCP=NP/NC