Задача 59886 ‹ — Ы e B R я ...
Условие
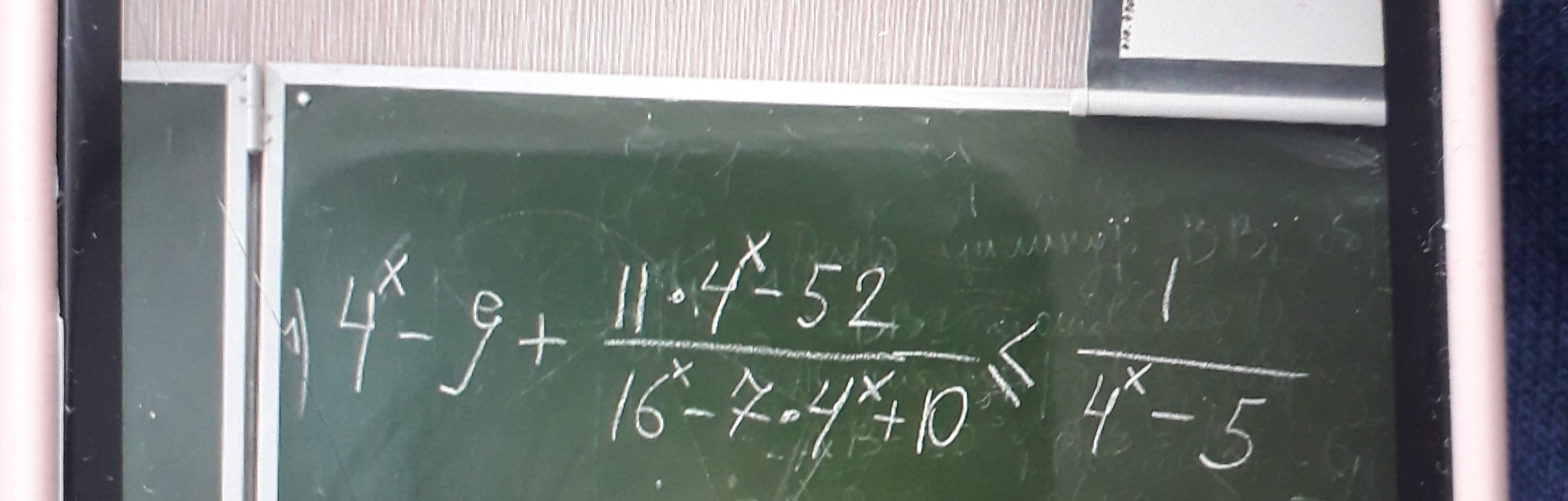
математика
479
Решение
★
[m]4^{x}=t[/m]
[m]16^{x}=t^2[/m]
Неравенство:
[m]t-9+\frac{11t-52}{t^2-7t+10} ≤ \frac{1}{t-5}[/m]
[m]t^2-7t+10=(t-2)(t-5)[/m]
[m]t-9+\frac{11t-52}{(t-5)(t-2)} - \frac{1}{t-5} ≤ 0[/m]
[m]t-9+\frac{11t-52-t+2}{(t-5)(t-2)} ≤ 0[/m]
[m]t-9+\frac{10t-50}{(t-5)(t-2)} ≤ 0[/m]
[m]t-9+\frac{10(t-5)}{(t-5)(t-2)} ≤ 0[/m]
[m]t-9+\frac{10}{(t-2)} ≤ 0[/m]
t ≠ 5
[m]\frac{(t-9)(t-2)+10}{(t-2)} ≤ 0[/m]
...