Задача 598 В правильной четырехугольной пирамиде...
Условие
математика 10-11 класс
8873
Решение
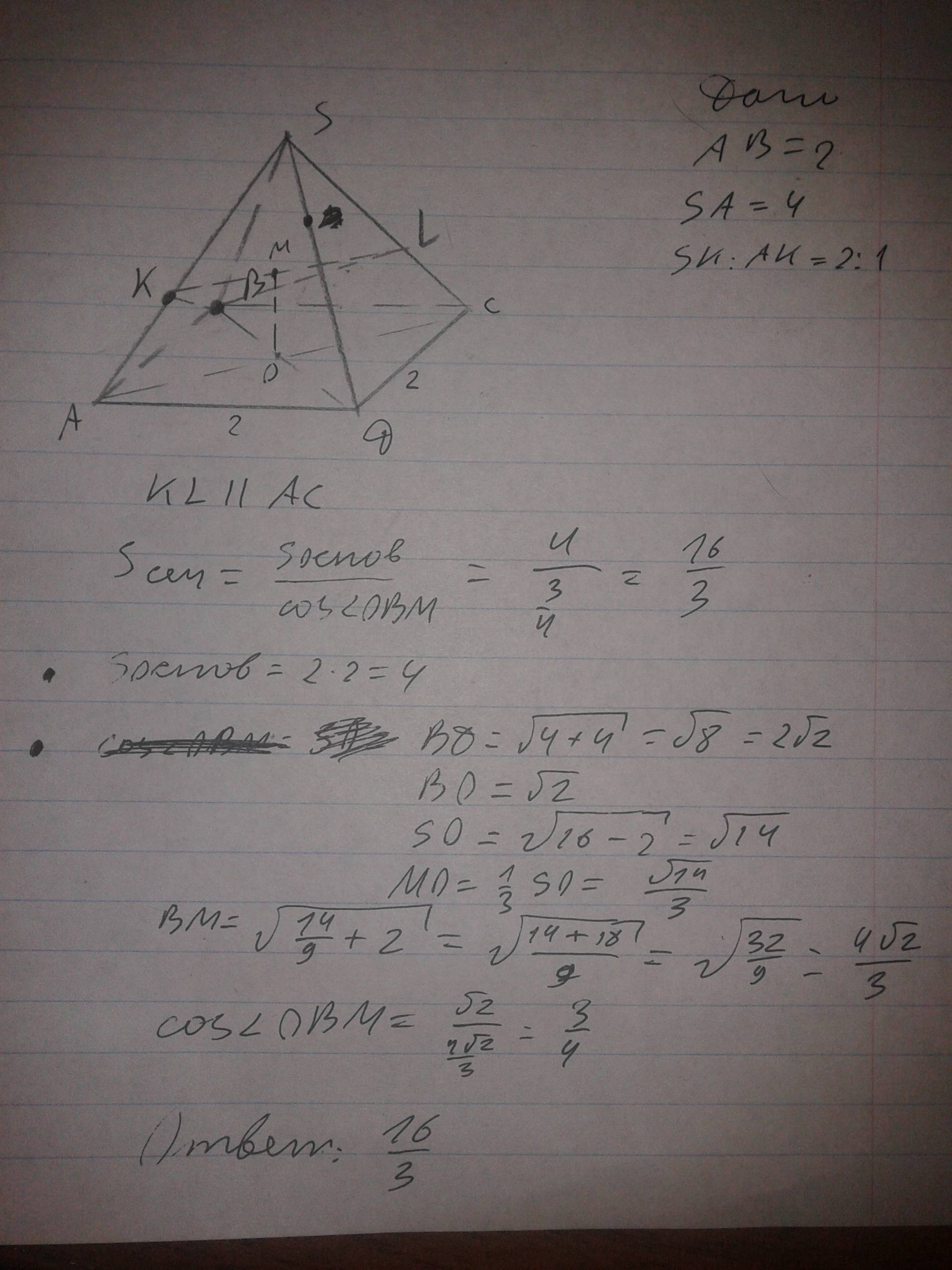
Ответ: 16/3
Все решения
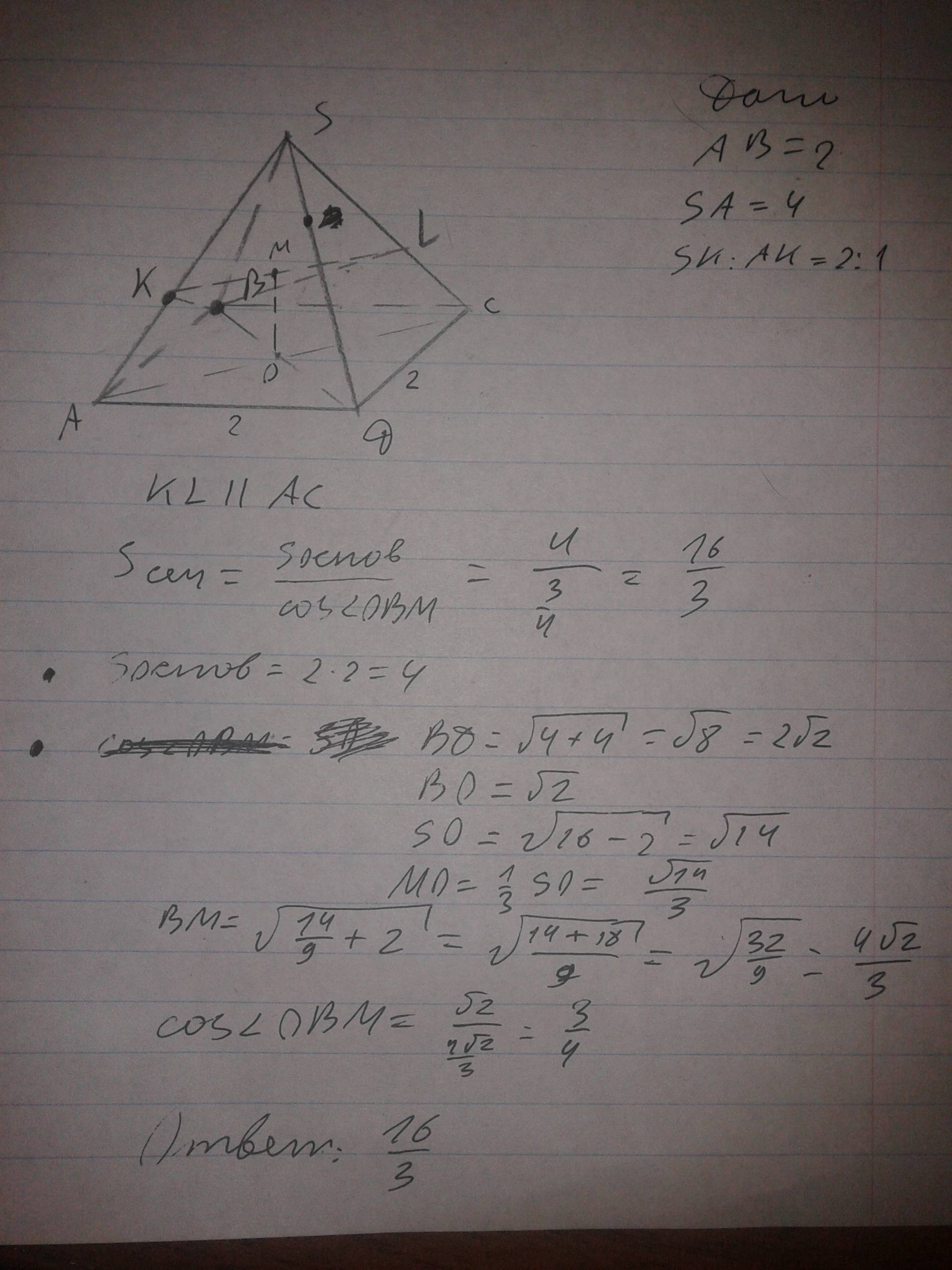
Ответ: 16/3