Задача 59774 Ровно в полдень из посёлка выехал...
Условие
Решение
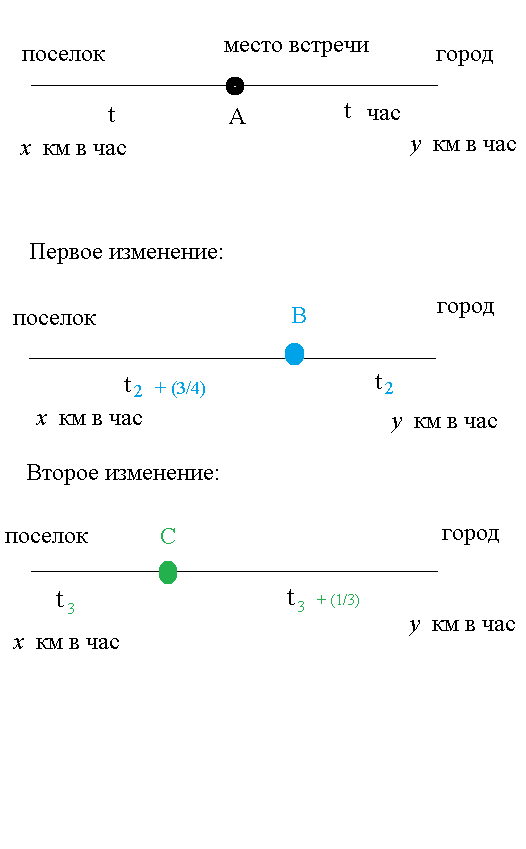
Пусть скорость грузовика х км в час
скорость автомобиля у км в час
Грузовик проехал путь tx км
Автомобиль проехал путь ty км
Первое изменение:
Автомобиль находился в пути t_(2) часов и проехал путь
t_(2)*y км
Грузовик находился в пути на 45 мин=(3/4) часа больше, т. е (t_(2)+(3/4)) часа и проехал путь
(t_(2)*x + (3/4) x) км
По условию
t_(2)y < ty на 36 км ⇒ ty=t_(2)y+36 ⇒ [m] t_{2}=t-\frac{36}{y}[/m]
Тогда
t_(2)x+(3/4)x=tx+36 ⇒ [m] t_{2}+\frac{3}{4}=t+\frac{36}{x}[/m]⇒ [m] t_{2}=t+\frac{36}{x}-\frac{3}{4}[/m]
Приравниваем правые части и получаем:
[m]t-\frac{36}{y}= t+\frac{36}{x}-\frac{3}{4}[/m]⇒
[blue] [m] \frac{36}{x}+\frac{36}{y}=\frac{3}{4}[/m] [/blue]
Второе изменение
Грузовик находился в пути t_(3) часов и проехал путь
t_(3)*х км
Автомобиль находился в пути на 20 мин=(1/3) часа больше, т. е (t_(3)+(1/3)) часа и проехал путь
(t_(3)*y+(1/3)y) км
По условию
t_(3)x < tx на k км ⇒ [m] t_{3}x+k=tx[/m]⇒ [m]t_{3}=t-\frac{k}{x}[/m]
и
[m]t_{3}y+\frac{1}{3}y=ty+k[/m]⇒ [m] t_{3}+\frac{1}{3}=t+\frac{k}{y}[/m]⇒ [m] t_{3}=t+\frac{k}{y}-\frac{1}{3}[/m]
[m]t-\frac{k}{x}=t+\frac{k}{y}-\frac{1}{3}[/m]
Значит, [m] \frac{k}{x}+\frac{k}{y}=\frac{1}{3}[/m]
Используем первое равенство:
[blue] [m] \frac{36}{x}+\frac{36}{y}=\frac{3}{4}[/m] [/blue]
Делим на 3:
[m] \frac{12}{x}+\frac{12}{y}=\frac{1}{4}[/m] ⇒
Умножаем на 4:
[m] \frac{48}{x}+\frac{48}{y}=1[/m] ⇒
Делим на 3:
[m] \frac{16}{x}+\frac{16}{y}=\frac{1}{3}[/m]
Сравнивая это равенство с равенством [m] \frac{k}{x}+\frac{k}{y}=\frac{1}{3}[/m]
заключаем, что
[red]k=16[/red]