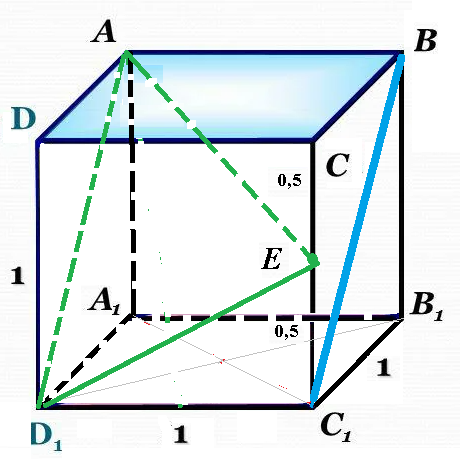
Задача 59619 В единичном кубе ABCDA1B1C1D1 найдите...
Условие
Решение
BC_(1) || пл AD_(1)E
Расстояние между прямой AE и ВС_(1) равно расстоянию между прямой BC_(1) и плоскостью AD_(1)E
Требуется построить перпендикуляр к плоскости AD_(1)E из любой точки прямой ВС_(1)
Не просто это сделать.
Поэтому
Решаю координатным методом.
Вводим координаты:
A_(1)(0;0;0); D_(1)(1;0;0); B_(1)(0;1;0); C_(1)=(1;1;0)
A(0;0;1); D(1;0;1); B(0;1;1); C(1;1;1)
E(1;1;0,5)
Уравнение плоскости АD_(1)E имеет вид :[b][i]ax+by+cz+d=0[/i][/b]
A(0;0;1): [b][i]c+d=0[/i][/b] ⇒ d=-c
D_(1)(1;0;0):[b][i]a+d=0[/i][/b] ⇒ d=-a
E(1;1;0,5):[b][i]a+b+0,5c+d=0[/i][/b] ⇒ a=c; d=-c
[b][i]c+b+0,5c-c=0[/i][/b] ⇒ b=-0,5c
[b][i]cx-0,5cy+cz-c=0[/i][/b]
Делим на с:
x-0,5y+z-1=0
Формула расстояния от точки до плоскости ( см. скрин)
ρ (B, пл AD_(1)E)=[m]\frac{|0-0,5\cdot 1+1-1|}{\sqrt{1+(-0,5)^2+1}}=\frac{0,5}{1,5}=\frac{1}{3}[/m]
можно найти
ρ (С_(1), пл AD_(1)E)=[m]\frac{|1-0,5\cdot 1+0-1|}{\sqrt{1+(-0,5)^2+1}}=\frac{|-0,5|}{1,5}=\frac{1}{3}[/m]