Задача 58684 ...
Условие
∫ P_n(x) / y dx = Q_n-1 (y) + λ ∫ dx / y ,
где y = √(ax^2 + bx + c), P_n(x) — многочлен степени n, Q_n-1 (x) — многочлен степени n-1 и λ — число, найти следующие интегралы:
∫ x^2√(a^2 - x^2) dx.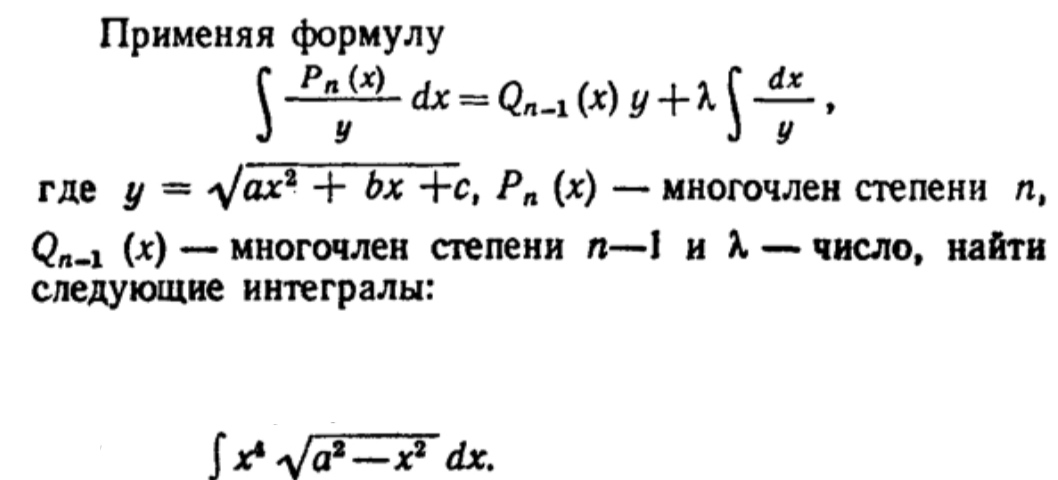
Решение
[m] ∫ x^4\cdot \sqrt{a^2-x^2}dx=∫ x^4\cdot \frac{(a^2-x^2)}{\sqrt{a^2-x^2}}dx= ∫\frac{a^2x^4-x^6}{\sqrt{a^2-x^2}}dx= [/m]
что можно записать как разность двух дробей
[m]=a^2∫\frac{x^4}{\sqrt{a^2-x^2}}dx-∫\frac{x^6}{\sqrt{a^2-x^2}}dx= [/m]
Каждый интеграл считаем по приведенной в условии формуле
1)
[m]∫\frac{x^4}{\sqrt{a^2-x^2}}dx[/m]
[m]y=\sqrt{a^2-x^2}[/m]
P(x)=x^4
Q(x)=x^3
[m]∫\frac{x^4}{\sqrt{a^2-x^2}}dx=x^3\cdot \sqrt{a^2-x^2}+ λ ∫\frac{dx}{ \sqrt{a^2-x^2}}[/m]
Дифференцируем обе части равенства и находим λ
[m]\frac{x^4}{\sqrt{a^2-x^2}}=3x^2\cdot \sqrt{a^2-x^2}+x^3\cdot \frac{(-2x)}{2\sqrt{a^2-x^2}}+ λ \frac{1}{ \sqrt{a^2-x^2}}[/m]
[m]\frac{x^4}{\sqrt{a^2-x^2}}=3x^2\cdot \sqrt{a^2-x^2}-\frac{x^4}{\sqrt{a^2-x^2}}+ λ \frac{1}{ \sqrt{a^2-x^2}}[/m]
[m]\frac{2x^4}{\sqrt{a^2-x^2}}-3x^2\cdot \frac{(a^2-x^2)}{\sqrt{a^2-x^2}}= λ \frac{1}{ \sqrt{a^2-x^2}}[/m] ⇒
[m] λ =?[/m]
[blue][m]∫\frac{x^4}{\sqrt{a^2-x^2}}dx=x^3\cdot \sqrt{a^2-x^2}+(?)arcsinx[/m]
[/blue]
2)
[m]∫\frac{x^6}{\sqrt{a^2-x^2}}dx[/m]
[m]y=\sqrt{a^2-x^2}[/m]
P(x)=x^6
Q(x)=x^5
[m]∫\frac{x^6}{\sqrt{a^2-x^2}}dx=x^5\cdot \sqrt{a^2-x^2}+ λ ∫\frac{dx}{ \sqrt{a^2-x^2}}[/m]