Задача 585 Найдите наибольшее значение функции...
Условие
математика 10-11 класс
65997
Решение
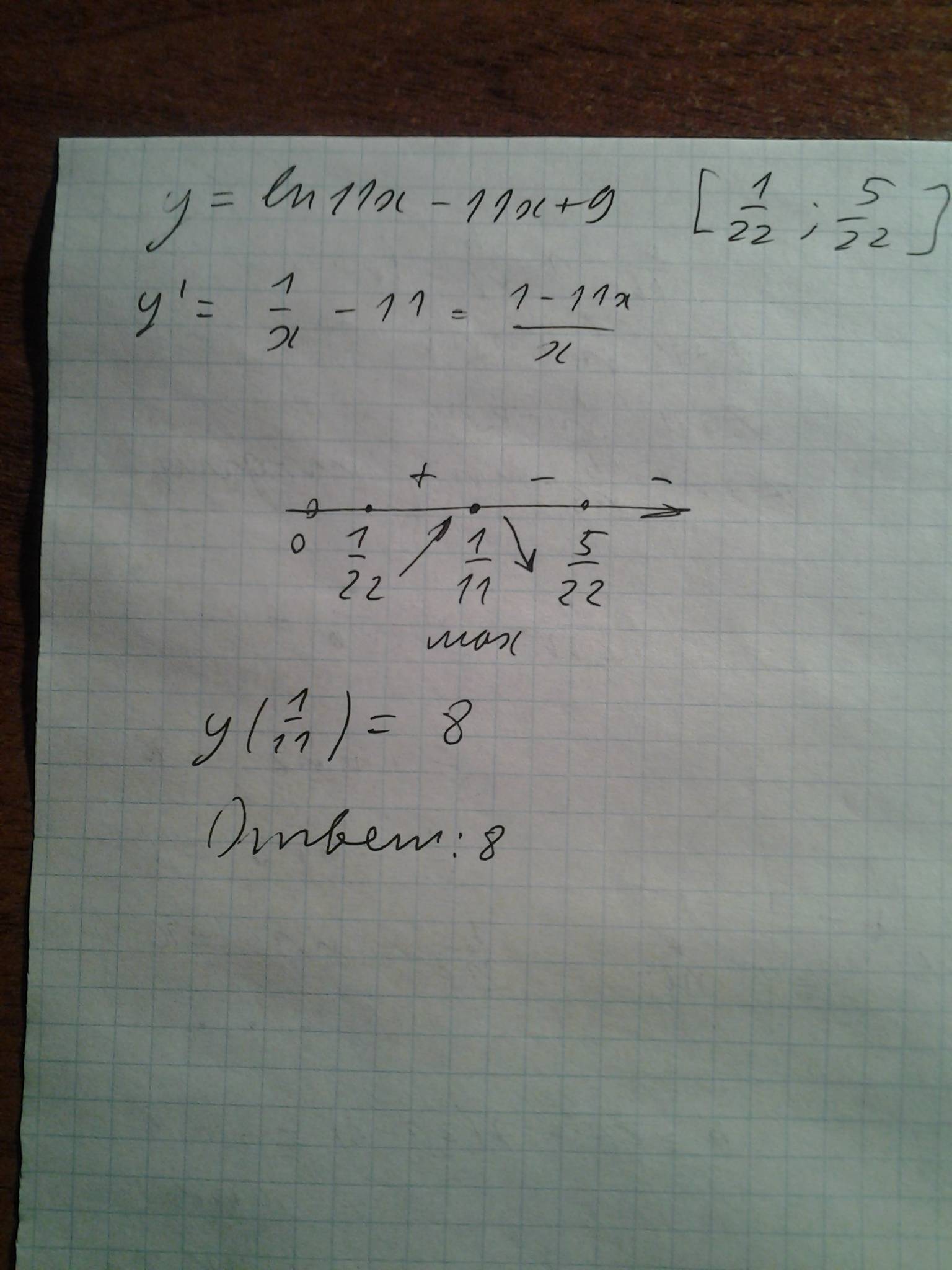
Ответ: Не как на картинке
Все решения
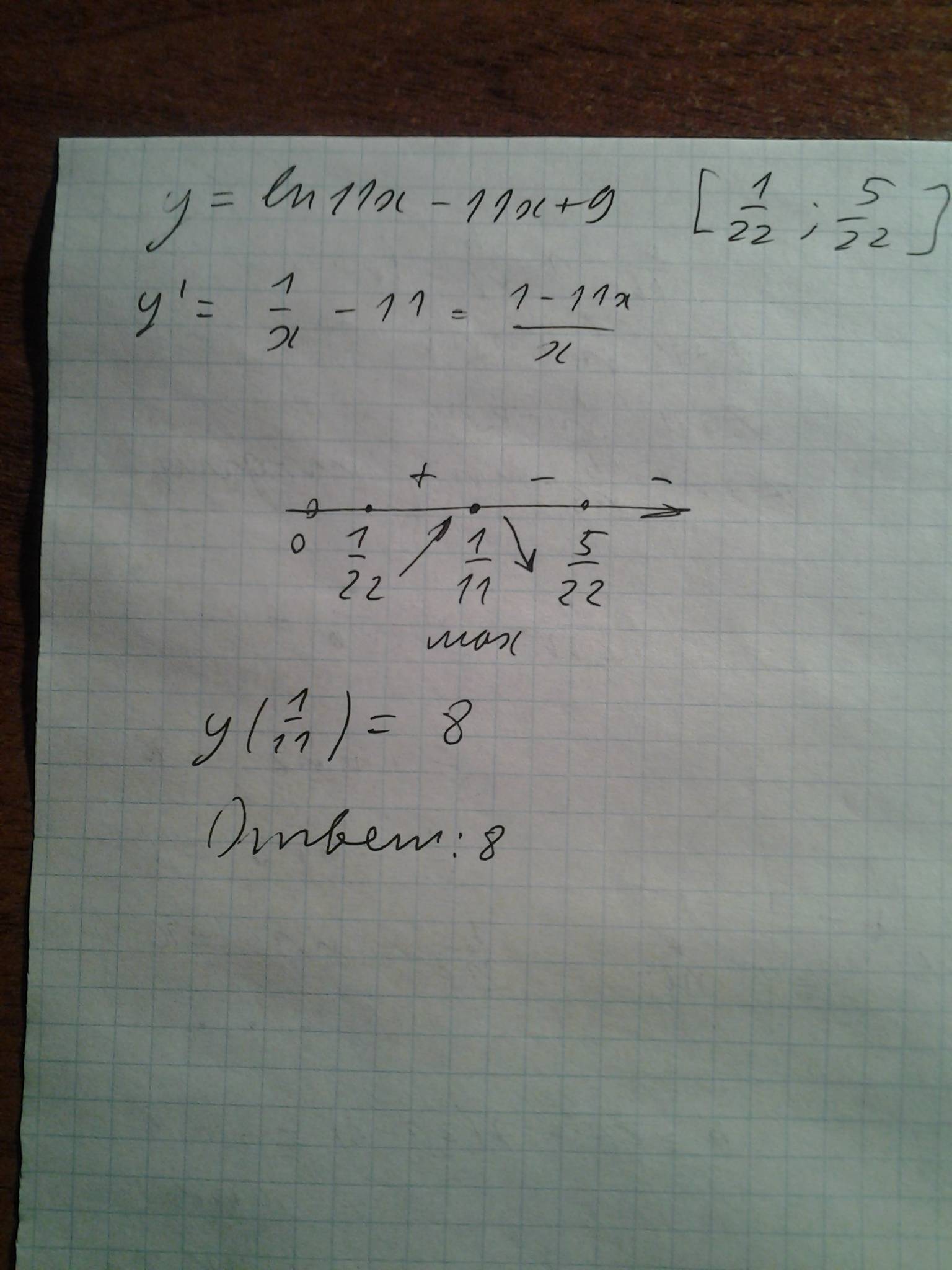
Ответ: Не как на картинке