Задача 58165 ...
Условие
-2 ≤ x 8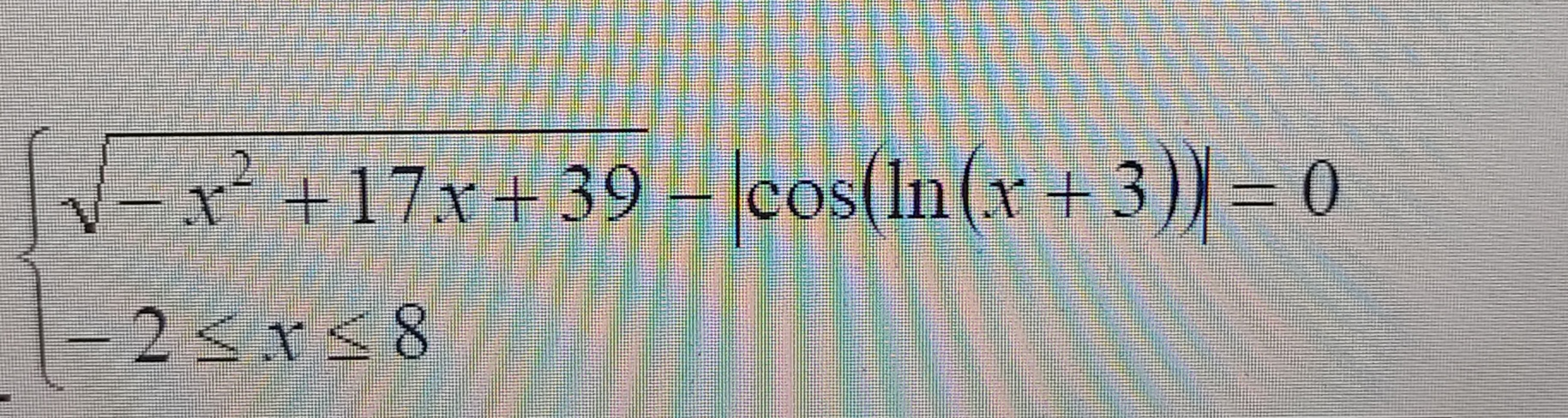
математика 10-11 класс
647
Решение
★
-1 ≤ cos(ln(x+3)) ≤ 1 ⇔ |cos(ln(x+3))| ≤ 1
Дан промежуток [-2;8]
На этом промежутке :
1= sqrt(-2^2+17*(-2)+39) [b]≤[/b] sqrt(-x^2+17x+39) ≤ sqrt(-8^2+17*8+39)
Наименьшее значение функция y=sqrt(-x^2+17x+39) принимает в точке х=-2.
Наибольшее значение функции y= |cos(ln(x+3))| равно 1
Поэтому уравнение имеет решение только в случае:
[m]\left\{\begin {matrix}\sqrt(-x^2+17x+39) =1\\|cos(ln(x+3))|=1\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}x =-2 ∈ ОДЗ \\|cos(ln(x+3))|=1\end {matrix}\right.[/m]