Задача 58062 Решая неравенство (см рисунок) на основе...

valera200990@rambler.ru

23 февраля 2021 г. в 14:10

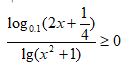
Решая неравенство (см рисунок) на основе понятия «дробь неотрицательна, если…» ученик получил в ответе, что данное неравенство не имеет решения. Указать на ошибки в решении ученика (если таковые имелись). Привести верное решение по этому способу.

exponenta

23 февраля 2021 г. в 14:42

★

Решение неравенства на основе свойства дроби:
«дробь неотрицательна, если…»

состоит в решении системы двух неравенств:
[m]\left\{\begin {matrix}log_{0,1}(2x+\frac{1}{4}) ≥ 0\\lg(x^2+1)>0\end {matrix}\right.[/m] или [m]\left\{\begin {matrix}log_{0,1}(2x+\frac{1}{4}) ≤ 0\\lg(x^2+1)<0\end {matrix}\right.[/m]

Но обязательно наличие ОДЗ в каждой, т.е

[m]\left\{\begin {matrix}2x+\frac{1}{4}>0\\x^2+1>0\\log_{0,1}(2x+\frac{1}{4}) ≥ 0\\lg(x^2+1)>0\end {matrix}\right.[/m] или [m]\left\{\begin {matrix}2x+\frac{1}{4}>0\\x^2+1>0\\log_{0,1}(2x+\frac{1}{4}) ≤ 0\\lg(x^2+1)<0\end {matrix}\right.[/m]

x² ≥ 0

x²+1 >0 при любом х


[m]\left\{\begin {matrix}x>-\frac{1}{8}\\log_{0,1}(2x+\frac{1}{4}) ≥ log_{0,1}1\\lg(x^2+1)>lg1\end {matrix}\right.[/m] или [m]\left\{\begin {matrix}x>-\frac{1}{8}\\log_{0,1}(2x+\frac{1}{4}) ≤ log_{0,1}1\\lg(x^2+1)<lg1\end {matrix}\right.[/m]

Применяем свойство убывания логарифмической функции с основанием 0,1 < 1 и возрастания логарифмической функции с основанием 10

[m]\left\{\begin {matrix}x>-\frac{1}{8}\\2x+\frac{1}{4} ≤ 1\\x^2+1>1\end {matrix}\right.[/m] или [m]\left\{\begin {matrix}x>-\frac{1}{8}\\2x+\frac{1}{4} ≥ 1\\x^2+1<1\end {matrix}\right.[/m]

[m]\left\{\begin {matrix}x>-\frac{1}{8}\\x≤ \frac{3}{8}\\x^2>0\Rightarrow x ≠ 0\end {matrix}\right.[/m] или [m]\left\{\begin {matrix}x>-\frac{1}{8}\\x ≥ \frac{3}{8} \\x^2<0 - неверно\end {matrix}\right.[/m]

Вторая система не имеет решений.

Решение первой является ответом

О т в е т. [m](-\frac{1}{8};0)\cup(0; \frac{3}{8}][/m]