Задача 57813 Алгебра. 10 класс. Необходимо решение....
Условие
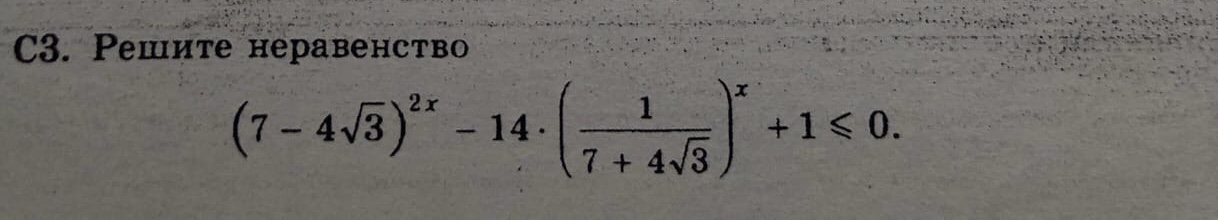
математика 10-11 класс
566
Решение
★
[m]7-4\sqrt{3}=\frac{1}{7+4\sqrt{3}}[/m]
[m](\frac{1}{7+4\sqrt{3}})^{x}=(7-4\sqrt{3})^{x}[/m]
Замена переменной:
[m](7-4\sqrt{3})^{x}=t[/m] ⇒
[m](\frac{1}{7+4\sqrt{3}})^{x}=t[/m]
[m](7-4\sqrt{3})^{2x}=t^2[/m]
Неравенство принимает вид:
[m]t^2-14t+1 ≤ 0[/m]
D=196-4=192
t=7 ± sqrt(3)
Решение неравенства
7-4sqrt(3) ≤ t ≤ 7+4sqrt(3)
Обратный переход:
[m]7-4\sqrt{3} ≤ (7-4\sqrt{3})^{x} ≤ 7+4\sqrt{3}[/m]
Показательная функция с основанием:
[m]0<7-4\sqrt{3} <1[/m] убывающая.
Поэтому:
[m]-1 ≤ x ≤ 1[/m]