Задача 57432 Найдите векторно-параметрическое...
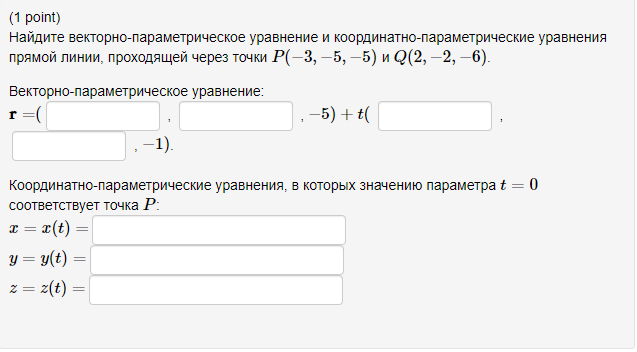
Условие
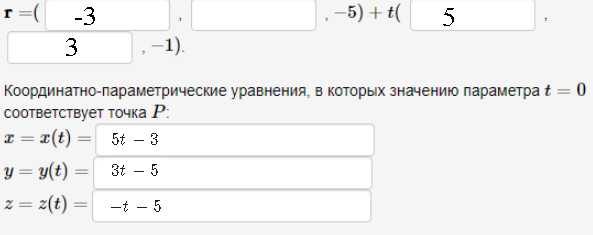
Векторно-параметрическое уравнение:
Координатно-параметрические уравнения, в которых значению параметра t = 0 соответствует точка P:
Решение
[m]\frac{x-(-3)}{2-(-3)}=\frac{y-(-5)}{-2-(-5)}=\frac{z-(-5)}{-6-(-5)}[/m]
Параметризуем ( вводим параметр):
[m]\frac{x-(-3)}{2-(-3)}=\frac{y-(-5)}{-2-(-5)}=\frac{z-(-5)}{-6-(-5)}[/m]= [b]t[/b] ⇒
[m]\frac{x-(-3)}{2-(-3)}[/m]= [b]t[/b] ⇒ x+3=5t
[m]x=5t-3[/m]
\frac{y-(-5)}{-2-(-5)}[/m]= [b]t[/b] ⇒ y+5=3t
[m]y=3t-5[/m]
\frac{z-(-5)}{-6-(-5)}[/m]= [b]t[/b] ⇒ z+5=-t
[m]z=-t-5[/m]