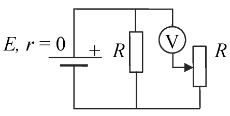
Задача 573 В схеме на рисунке сопротивление...
Условие
физика 10-11 класс
11369
Решение

Ответ: в решение


Ответ: в решение