Задача 572 Рамку с постоянным током...
Условие
Ответ поясните, указав, какие физические закономерности вы использовали для объяснения. Считать, что рамка испытывает небольшое сопротивление движению со стороны воздуха.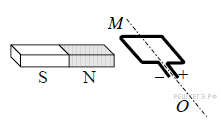
Решение
2) Рассмотрим сечение рамки плоскостью рисунка в условии задачи. В исходном положении в левом звене рамки ток направлен к нам, а в правом — от нас. На левое звено рамки действует сила Ампера , направленная вверх, а на правое звено — сила Ампера , направленная вниз.
Эти силы разворачивают рамку на неподвижной оси MO по часовой стрелке (см. рисунок).
3) Рамка устанавливается перпендикулярно оси магнита так, что контакт «+» оказывается внизу. При этом силы Ампера и обеспечивают равновесие рамки на оси MO (см. рисунок).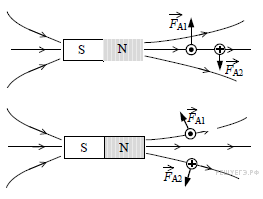
Ответ: в решение