Задача 571 Две порции одного и того же...
Условие
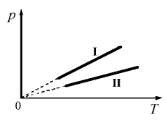
физика 10-11 класс
14373
Решение

Ответ: в решение


Ответ: в решение