Задача 569 По первому закону Столетова...
Условие
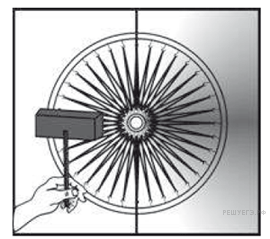
Решение
2. При этом центр тяжести колеса сместится вправо, и появится момент силы тяжести относительно оси колеса, стремящийся повернуть колесо вправо.Равновесие колеса нарушится, и оно начнёт вращаться по часовой стрелке.
3. При вращении колеса нагретые резинки будут удаляться от лампы и охлаждаться за счет теплообмена с окружающей средой, а ненагретые резинки будут приближаться к лампе и нагреваться её излучением. Описанные процессы будут повторяться. В результате колесо будет непрерывно вращаться, если нагретые резинки за время его оборота будут успевать достаточно охладиться.
Ответ: в решение