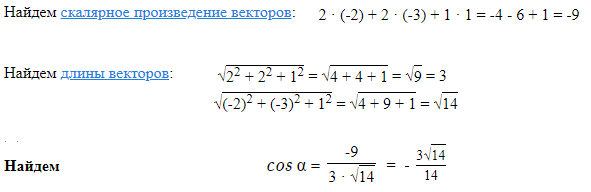Задача 56801 Контрольная работа 2. Векторная...

5ff85d20960c3c35933da9b2

08.01.2021 21:55:24

Контрольная работа 2. Векторная алгебра

Задача 1. Даны точки A, B, C. Разложить вектор a по ортам i, j, k. Найти длину, направляющие косинусы и орт вектора a. Найти косинус угла, образованного вектором AC и AB.

A (4; 1; 0); B (2; -2; 1); C (6; 3; 1).

a = AB + CB.

5f3ea7e3faf909182968ddd9

08.01.2021 23:07:20

★

vector{AB}=(2-4;-2-1;1-0)=(-2;-3;1)

vector{CB}=(2-6;(-2)-3;1-1)=(-4;-5;0)

vector{a}=vector{AB}+vector{CB}=(-2-4;-3-5;1+0)=(-6;-8;1) ⇒
vector{a}=-6vector{i}-8vector{j}+1vector{k} - разложение по ортам.

|vector{a}|=sqrt((-6)^2+(-8)^2+1^2)=sqrt(101) - длина вектора vector{a}

Направляющие косинусы:

cos α =-6/sqrt(101)

cos β =-8/sqrt(101)

cos γ =1//sqrt(101)


vector{AB}=(2-4;-2-1;1-0)=(-2;-3;1)
vector{AС}=(6-4;3-1;1-0)=(2;2;1)