Задача 568 В установке по наблюдению...
Условие
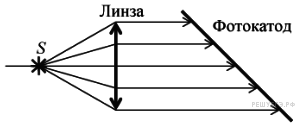
Решение
По первому закону Столетова фототок насыщения зависит от интенсивности падающего света, то есть от количества фотонов, падающих на фотокатод в единицу времени. При использовании линзы такого же диаметра, но с меньшим фокусным расстоянием, телесный угол, под которым из источника видно линзу, увеличивается. Фотоны летят от источника во все стороны равномерно, поэтому результирующий поток фотонов, попадающих на фотокатод в результате замены линзы, увеличивается. А значит, увеличивается и ток насыщения.
Ответ: в решение