Задача 56579 Диференциальное уравнение, помогите с...
Условие
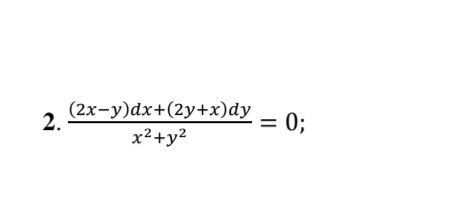
Решение
P(x;y)=(2x-y)/(x^2+y^2);
Q(x;y)=(2y+x)/(x^2+y^2).
Так как
∂ P/ ∂ y=(-1*(x^2+y^2)-2y*(2x-y))/(x^2+y^2)^2
∂ Q/ ∂ x=(-1*(x^2+y^2)-2y*(2x-y))/(x^2+y^2)^2.
и ∂ P/ ∂ y = ∂ Q/ ∂ x,
то это [b]уравнение в полных дифференциалах.[/b]
Значит, u(x;y)=C - решение дифференциального уравнения.
Функция u может быть найдена из условий:
∂ u/ ∂ x=P(x;y)
∂ u/ ∂ y=Q(x;y)
∂ u/ ∂ x=P(x;y) ⇒ [b]u(x;y)[/b]= ∫ P(x;y) dx= ∫ (2x-y)/(x^2+y^2)dx=∫ (2xdx)/(x^2+y^2)-∫ (y·dx)/(x^2+y^2)=
=ln(x^2+y^2)-arctg(x/y)+ [b]φ (y)[/b]
Находим производную:
∂ u/ ∂ y=(ln(x^2+y^2)-arctg(x/y)+ [b]φ (y)[/b])`_(y)=(ln(x^2+y^2))`_(y)-(arctg(x/y))`_(y)+ [b](φ (y)[/b])`_(y)=
=2y/(x^2+y^2)-(1)/(1+(x/y)^2))*(x/y)`_(y)+φ`(y)=2y/(x^2+y^2) + (x)/(x^2+y^2)+[b]φ` (y)[/b]
Так как
∂ u/ ∂ y=Q(x;y)
то
[b]φ` (y)[/b]=0
Тогда
[b] φ (y)[/b]=C
О т в е т.
u(x;y)=ln(x^2+y^2)-arctg(x/y)+C
