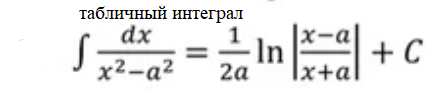Задача 56446 Найти длину дуги кривой [m] y = e^x + 13...
Условие
Решение
[m]1+(f`(x))^2=1+e^{2x}[/m]
[m]L= ∫ ^{ln\sqrt{24}}_{ln\sqrt{15}}\sqrt{1+e^{2x}}dx=[/m]
Замена переменной:
[m]\sqrt{1+e^{2x}}=t[/m] ⇒[m]1+e^{2x}=t^2[/m] ⇒[m]e^{2x}=t^2-1[/m] ⇒
[m] 2x=ln(t^2-1)[/m]
[m]dx=\frac{2t}{2(t^2-1)}dt[/m]
[m]dx=\frac{t}{t^2-1}dt[/m]
В неопределенном интеграле получим:
[m]∫ \sqrt{1+e^{2x}}dx= ∫ t\cdot \frac{t}{t^2-1}dt ∫ \frac{t^2-1+1}{t^2-1}dt= ∫dt+ ∫\frac{1}{t^2-1}dt =t+\frac{1}{2}ln|\frac{t-1}{t+1}|+C=\sqrt{1+e^{2x}}+\frac{1}{2}ln|\frac{\sqrt{1+e^{2x}}-1}{\sqrt{1+e^{2x}}+1}+С [/m]
Первообразная найдена!
Тогда
[m]L= ∫ ^{ln\sqrt{24}}_{ln\sqrt{15}}\sqrt{1+e^{2x}}dx=(\sqrt{1+e^{2x}}+\frac{1}{2}ln|\frac{\sqrt{1+e^{2x}}-1}{\sqrt{1+e^{2x}}+1})|^{ln\sqrt{24}}_{ln\sqrt{15}}[/m]
считайте