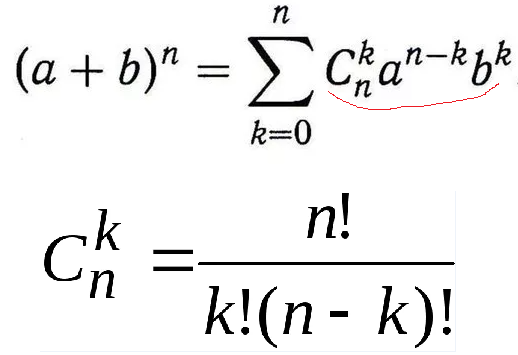Задача 56201 4. Найти биномиальный коэффициент члена...

5fd9e93cec9d2930a0897b23

16.12.2020 14:03:25

4. Найти биномиальный коэффициент члена разложения ... не содержащего a.

5f3ea7e3faf909182968ddd9

16.12.2020 14:30:34

★

k-ый член разложения бинома имеет вид ( cм. скрин)

[m]Т_{k}=C^{k}_{15}(\frac{x^2}{a})^{15-k}\cdot (\frac{a^2}{x})^{k}[/m]

k=0; 1; 2;... ;15

упрощаем:

[m]Т_{k}=C^{k}_{15}x^{2\cdot (15-k)-k}\cdot a^{2k-(15-k)}[/m]


По требованию задачи

[m]a^{2k-\cdot (15-k)}=a^{0}[/m]

⇒

[m]2k\cdot (15-k)=0[/m]

[m]k=5[/m]

Значит коэффициент равен [m]С^{5}_{15}[/m]

Считаем самостоятельно по формуле сочетаний ( cм. скрин)

Или в треугольнике Паскаля ( см скрин )

О т в е т. [m]С^{5}_{15}=3003[/m]