Задача 55850 Исследовать сходимость числового ряда а)...
Условие
а) знакопостоянного
б) знакопеременного.
Для знакопеременного ряда, если он совпадает, определить, какая
сходимость имеет место - абсолютная или условная.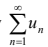

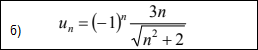
математика ВУЗ
272
Решение
★
[m] ∫^{+ ∞ }_{1}\frac{1}{(x+1)ln^2(x+1)}dx=∫^{+ ∞ }_{1}\frac{d(ln(x+1)}{ln^2(x+1)}=-\frac{1}{ln(x+1)}|^{+ ∞ }_{1}=0-(-\frac{1}{ln2})[/m]
2) Расходится, так как общий член ряда не стремится к нулю.
[m]lim_{n → ∞ }\frac{3n}{\sqrt{n^2+2}}=3[/m]