Задача 55837 Помогите пожалуйста, дайте решение....
Условие
Решение
x_(o)=1; x_(1)=1,4; x_(2)=1,8; x_(3)=2,2; x_(4)=2,6; x_(5)=3
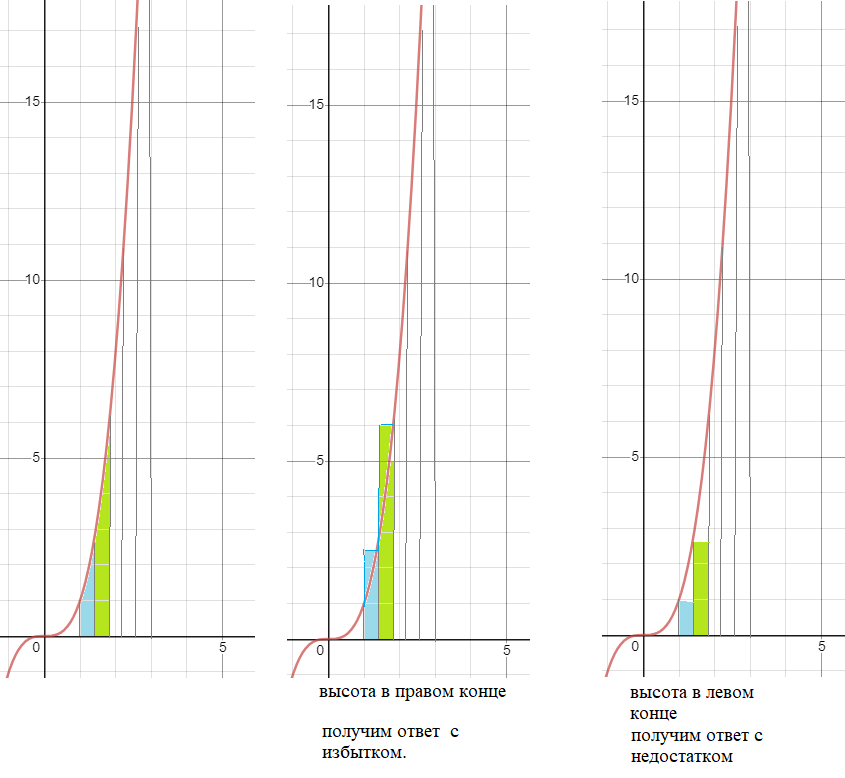
Получаем 5 криволиненых трапеций.
Заменим каждую прямоугольником
(cм. тему. Приближенное вычисление определенного интеграла. Способ прямоугольников.)
Получаем 5 прямоугольников
Основание каждого прямоугольника будет равно [m]\frac{2}{5}=0,4[/m]
Высота - значение в [b]правом конце каждого отрезка[/b]
([m]f(x)=x^3 [/m]⇒[m] (f(1,4)=1,4^3;f(1,8)=1,8^3;f(2,2)=2,2^3;f(2,6)=2,6^3;f(3)=3^3)[/m]
[m]∫ ^{3}_{1}x^3dx ≈ 1,4^3\cdot 0,4+1,8^3\cdot 0,4+2,2^3\cdot 0,4+2,6^3\cdot 0,4+3^3\cdot 0,4=[/m]
[m]=0,4\cdot (1,4^3+1,8^3+2,2^3+2,6^3+3^3)[/m]=считайте
( ответ получим с избытком)
Если высота - значение в [b]левом конце каждого отрезка[/b]
([m]f(x)=x^3 [/m]⇒[m] (а(1)=1^3; f(1,4)=1,4^3;f(1,8)=1,8^3;f(2,2)=2,2^3;f(2,6)=2,6^3)[/m]
[m]∫ ^{3}_{1}x^3dx ≈ 1^3\cdot 0,4+ 1,4^3\cdot 0,4+1,8^3\cdot 0,4+2,2^3\cdot 0,4+2,6^3\cdot 0,4=[/m]
[m]=0,4\cdot (1^3+1,4^3+1,8^3+2,2^3+2,6^3)[/m]=считайте
( ответ получим с недостатком)
Существует еще способ трапеций.
Вы не указали алгоритм, поэтому Вам и не решали....
Все решения
