Задача 55833 ...
Условие
lim (1-x)^(log₂ x)
x→1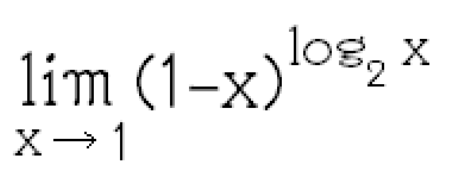
математика ВУЗ
335
Решение
★
Логарифмируем:
[m]lny=ln(1-x)^{log_{2}x}[/m]
Применяем свойство логарифма степени:
[m]lny=log_{2}x\cdot ln(1-x)[/m]
Находим предел:
[m]lim_{x →1} lny=lim_{x →1} log_{2}x\cdot ln(1-x)[/m] ⇒
[m]lim_{x →1} log_{2}x\cdot ln(1-x)=0\cdot ∞ [/m] неопределенность
Произведение u*v всегда можно представить в виде дроби: u/(1/v) или v/(1/u)
[m]lim_{x →1} log_{2}x\cdot ln(1-x)=lim_{x →1}\frac{ln(1-x)}{\frac{1}{log_{2}x}}[/m] получили неопределенность
( ∞ / ∞ ) и теперь можно применить правило Лопиталя:
[m]=lim_{x →1}\frac{(ln(1-x))`}{(\frac{1}{log_{2}x})`}= [/m] cчитайте...