Задача 55679 ПОЖАЛУЙСТА, ПРОШУ СРОЧНО...
Условие
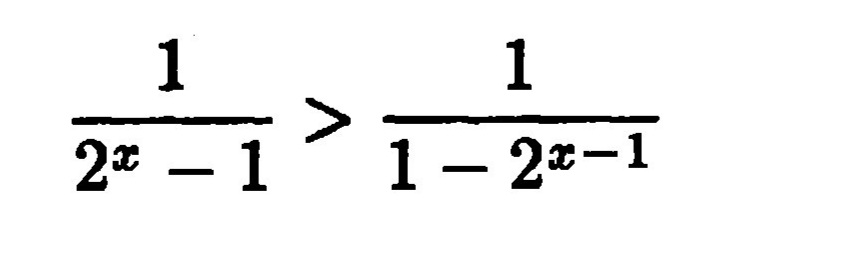
Решение
[m]2^{x-1}=t[/m]
t >0
[m]2^{x}=2^{x-1}\cdot 2=2\cdot t[/m]
Дробно рациональное неравенство:
[m]\frac{1}{2t-1}>\frac{1}{1-t}[/m]
Переносим влево:
[m]\frac{1}{2t-1}-\frac{1}{1-t}>0[/m]
меняем знак в знаменателе второй дроби и перед второй дробью:
[m]\frac{1}{2t-1}+\frac{1}{t-1}>0[/m]
приводим к общему знаменателю
[m]\frac{t-1+2t-1}{(2t-1)(t-1)}>0[/m]
упрощаем и получаем неравенство:
[m]\frac{3t-2}{(2t-1)(t-1)}>0[/m]
Решаем методом интервалов:
______ (1/2) ___[red]+[/red]___ (2/3) _____ (1) _____[red]+[/red]____
с учетом t > 0 получаем ответ
(1/2) < t < 2/3 или t > 1
Обратный переход:
[m]\frac{1}{2} < 2^{x-1}< \frac{2}{3}[/m] или [m]2^{x-1}>1[/m]
[m]2^{-1}< 2^{x-1}< \frac{2}{3}[/m] или [m]2^{x-1}>2^{0}[/m]
Показательная функция с основанием 2 >1 возрастающая, поэтому
[i]большему[/i] значению функции соответствует [i]большее [/i]значение аргумента:
[m] -1 < x-1< log_{2}\frac{2}{3}[/m] или [m]x-1 >0[/m]
[m] 0 < x<log_{2}\frac{2}{3}+1 [/m] или [m]x >1[/m]
От в е т. [m] (0 ; log_{2}\frac{2}{3}+1) [/m] U [m](1;+ ∞) [/m]
Что нужно знать и уметь, чтобы решать такие уравнения:
1) метод замены переменной
2) действия с дробями
3) метод интервалов
4) свойства показательной функции
5) логарифмы.