Задача 55579 Нужно решить "Уровнение и система...
Условие
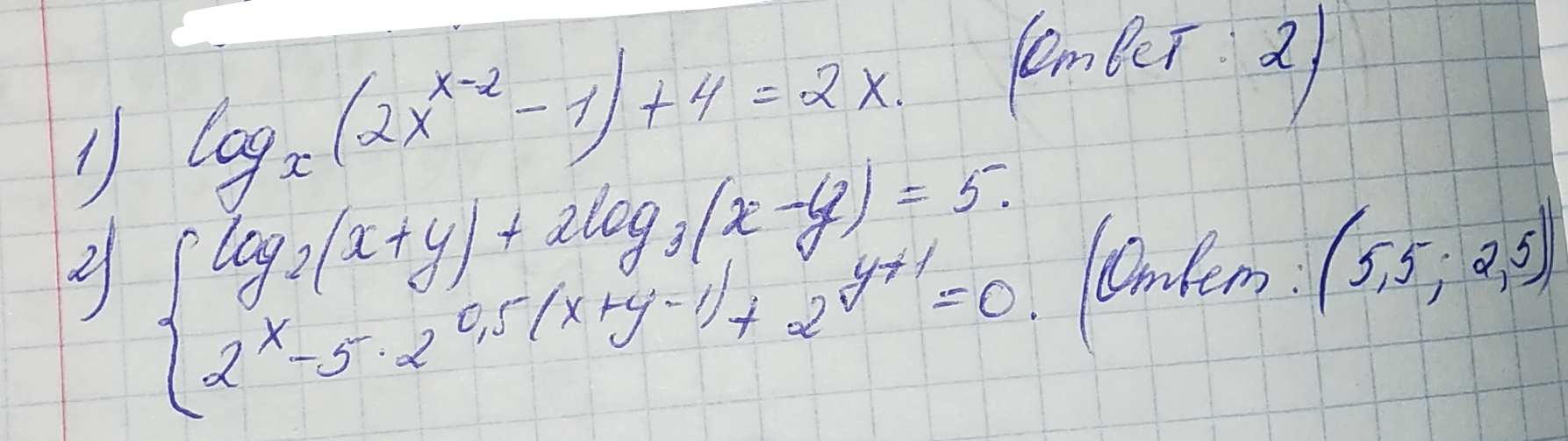
Решение
ОДЗ:
[m]\left\{\begin{matrix}
x>0\\x≠ 1\\2x^{x-2}-1>0 \end{matrix}\right.[/m]
[m]log_{x}(2x^{x-2}-1)=2x-4[/m]
[m]2x^{x-2}-1=x^{2x-4}[/m]
[m](x^{x-2})^2-2x^{x-2}+1=0[/m]
[m](x^{x-2}-1)^2=0[/m]
[m]x^{x-2}=1[/m]
Логарифмируем:
[m]lgx^{x-2}=lg1[/m]
[m](x-2)lgx=0[/m]
[m]x-2=0[/m] или [m]lgx=0[/m] ⇒ x=1 не входит в ОДЗ
[m]x=2[/m] удовлетворяет трем неравенствам в ОДЗ
[m]\left\{\begin{matrix}
2>0\\2≠ 1\\2\cdot 2^{2-2}-1>0 \end{matrix}\right.[/m]
О т в е т. 2
2)
[m]\left\{\begin{matrix}
log_{2}(x+y)\cdot (x-y)^3=5\\2^{x}-5\cdot 2^{0,5x}\cdot 2^{0,5y}\cdot 2^{-0,5}+2\cdot 2^{y}=0 \end{matrix}\right.[/m]
[m]2^{x}-5\cdot 2^{0,5x}\cdot 2^{0,5y}\cdot 2^{-0,5}+2\cdot 2^{y}=0[/m]
Замена:
[m] 2^{0,5x}=u[/m]; [m] 2^{0,5y}=v[/m] ⇒ [m] u^2-\frac{5}{\sqrt{2}}u\cdot v+2v^2=0[/m]
[m]D=(\frac{5}{\sqrt{2}}v)^2-4\cdot 2v^2=\frac{25}{2}v^2-8v^2=\frac{25-16}{2}v^2=\frac{9}{2}v^2[/m]
[m] u^2-\frac{5}{\sqrt{2}}u\cdot v+2v^2=(u-\frac{1}{\sqrt{2}}v)(u-\frac{4}{\sqrt{2}}v)[/m]
[m]\left\{\begin{matrix}
(x+y)\cdot (x-y)^3=2^5\\ (2^{0,5x}-\frac{1}{\sqrt{2}}2^{0,5y})(2^{0,5x}-\frac{4}{\sqrt{2}}2^{0,5y})=0\end{matrix}\right.[/m]
[m]\left\{\begin{matrix}
(x+y)\cdot (x-y)^3=2^5\\ 2^{0,5x}-\frac{1}{\sqrt{2}}2^{0,5y}=0\end{matrix}\right.[/m]или [m]\left\{\begin{matrix}
(x+y)\cdot (x-y)^3=2^5\\2^{0,5x}-\frac{4}{\sqrt{2}}2^{0,5y}=0 \end{matrix}\right.[/m]
[m]\left\{\begin{matrix}
(x+y)\cdot (x-y)^3=2^5\\ 2^{0,5x}=2^{0,5y-0,5}\end{matrix}\right.[/m]или [m]\left\{\begin{matrix}
(x+y)\cdot (x-y)^3=2^5\\2^{0,5x}=2^{0,5y+1,5} \end{matrix}\right.[/m]
[m]\left\{\begin{matrix}
(x+y)\cdot (x-y)^3=2^5\\0,5x=0,5y-0,5\end{matrix}\right.[/m]или [m]\left\{\begin{matrix}
(x+y)\cdot (x-y)^3=2^5\\0,5x=0,5y+1,5 \end{matrix}\right.[/m]
[m]\left\{\begin{matrix}
(x+y)\cdot (x-y)^3=2^5\\x=y-1\end{matrix}\right.[/m]или [m]\left\{\begin{matrix}
(x+y)\cdot (x-y)^3=2^5\\x=y+3 \end{matrix}\right.[/m]