Задача 55544 Построить график функции...

5fae1df5322e6f41f4eb67f7

13.11.2020 08:48:01

Построить график функции у=(х+4)(х2-4)/(х-2) и определить при каких значениях к прямая у=к имеет с графиком только одну общую точку

5f3ea7e3faf909182968ddd9

13.11.2020 09:39:18

★

Область определения:
x-2 ≠ 0
х ≠ 2

Так как x^2-4=(x-2)(x+2)
Сокращаем на (х-2) и числитель и знаменатель.

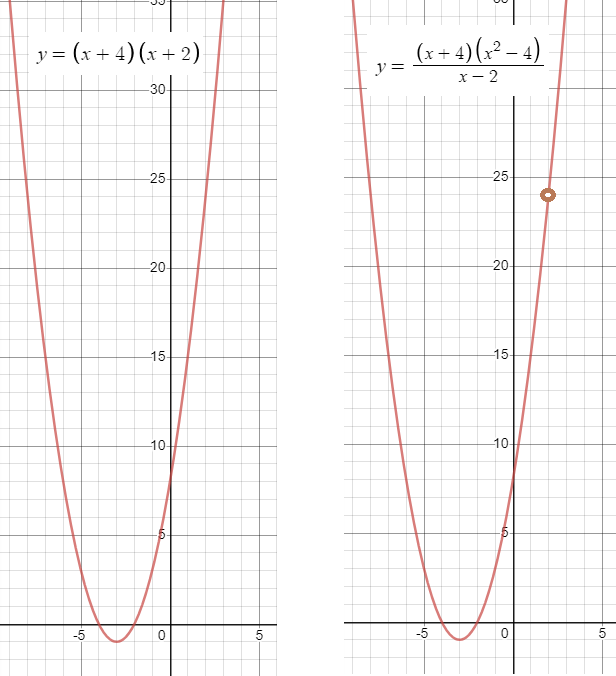
Получаем y=(x+4)*(x+2)

Эта функция определена при любых х, графиком является парабола

Функции y=(x+4)*(x^2-4)/(x-2) и y=(x+4)*(x+2) совпадают при всех х, кроме одной точки

x=2

Строим параболу
y=(x+4)*(x+2) на (- бесконечность;2)U(2;+ бесконечность),

т. е точку с абсциссой х=2, ординатой y=(2+4)*(2+2)=24 вырезаем.

На рисунке пустой кружок или "дырка"

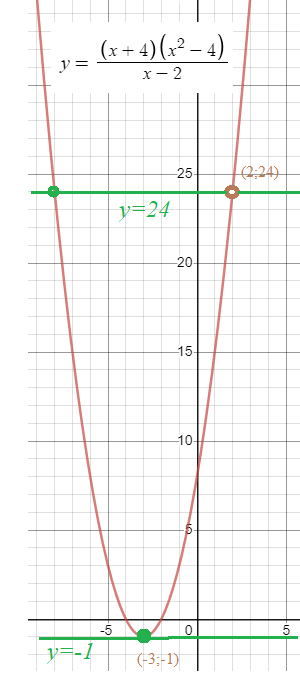
По рисунку видно, что прямая y=k параллельная оси Ох пересекает график функции y=(x+4)*(x^2-4)/(x-2) в одной точке в двух случаях:
если прямая проходит через вершину параболу (-3;[b]-1[/b]), т.е уравнение такой прямой y=[b]-1[/b]
и через точку (2;[b]24[/b]), т.е уравнение такой прямой y=[b]24[/b]







Ответ: -1; 24