Задача 55431 Завтра урок в зуме помогите пожалуйста ...
Условие
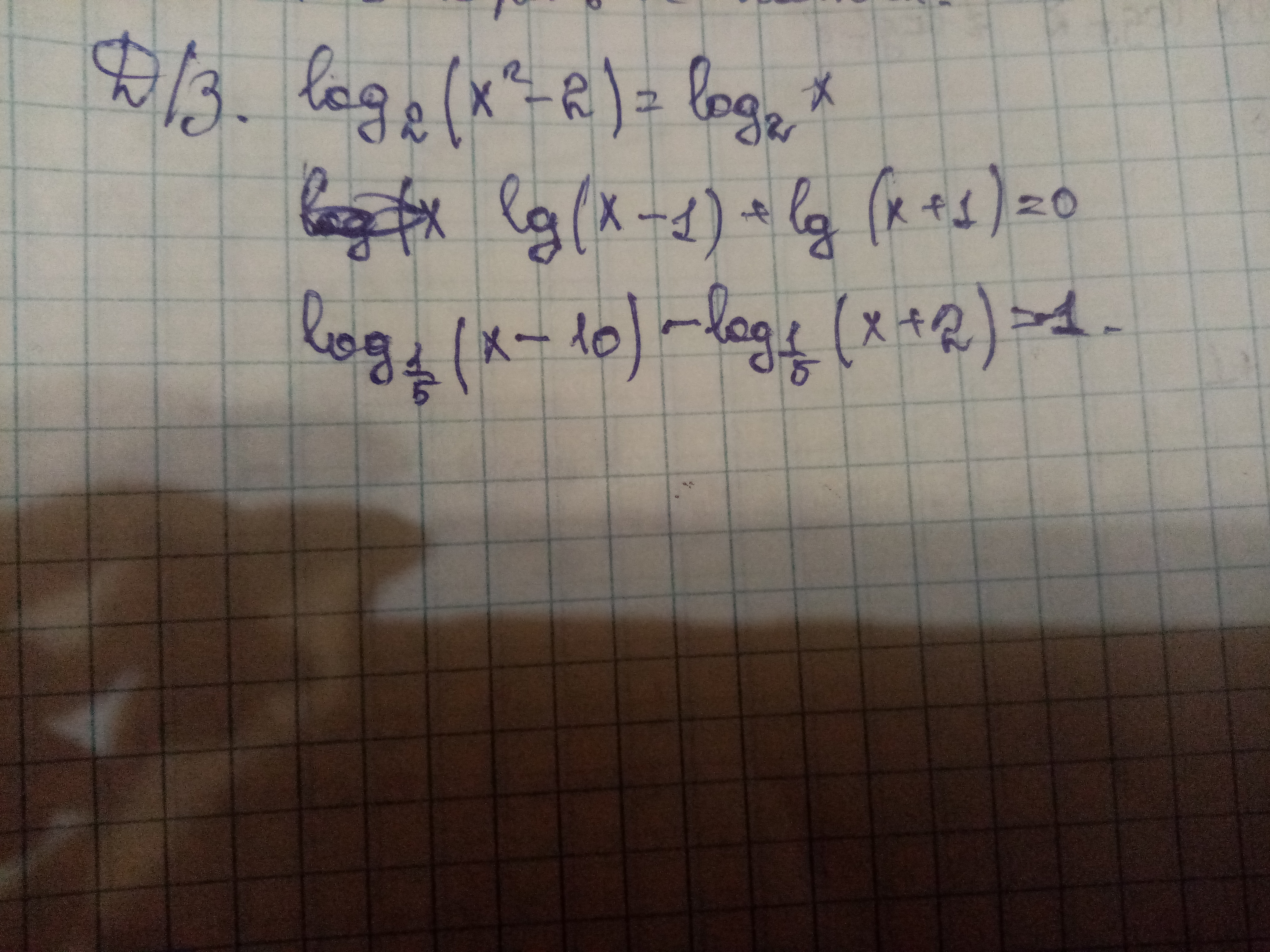
математика
602
Решение
★
Значит, если значения функции равны, то и аргументы равны:
x^2-2=x
x^2-x-2=0
D=1+8=9
x=-1 или x=2
Проверка:
При x=-1
lg((-1)^2-2) и lg(-1) не существуют. Значит х=-1 не является корнем уравнения
При x=2
lg(2^2-2)=lg2 - верно, так как lg2=lg2
О т в е т. х=2
[i]Второй способ[/i]
ОДЗ:
[m]\left\{\begin{matrix}
x^2-2 >0\\x>0 \end{matrix}\right.[/m]
На основании свойства монотонности логарифмической функции:
x^2-2=x
x^2-x-2=0
D=1+8=9
x=-1 или x=2
x=-1 не входит в ОДЗ: (-1)^2-2 >0 - неверно
x=2 входит в ОДЗ, оба неравенства верны
О т в е т. х=2