Задача 55218 Срочно! Система уровнений решите...
Условие
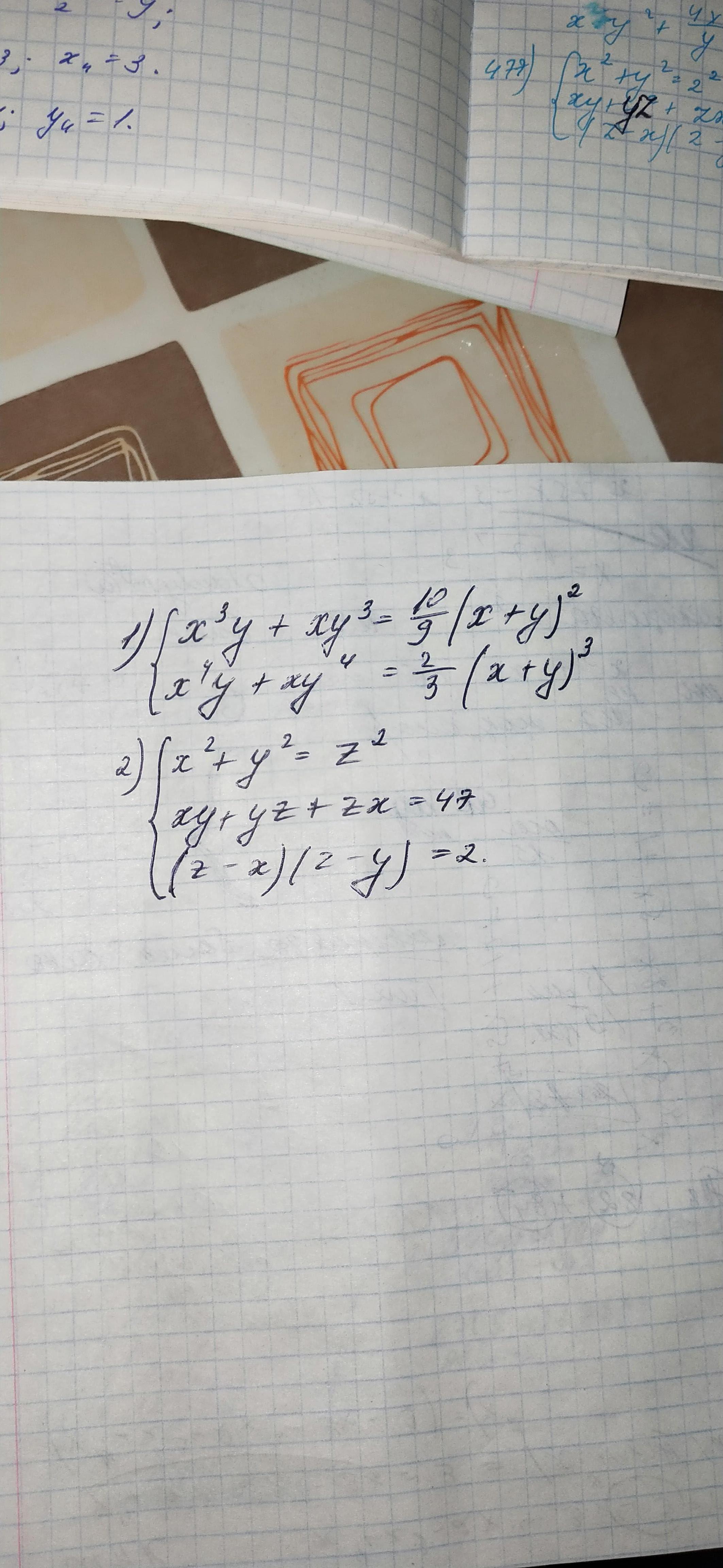
Решение
xy(x^2+y^2)=\frac{10}{9}(x+y)^2\\xy(x^3+y^3)=\frac{2}{3}(x+y)^3 \end{matrix}\right.[/m]
Замена переменной:
[m] x+y=u[/m];
[m] x\cdot y=v[/m].
Выразим
[m]x^2+y^2[/m] и [m]x^3+y^3[/m] через [m] u[/m] и [m] v[/m].
[m]x^2+y^2=(x+y)^2-2xy=u^2-2v[/m]
[m]x^3+y^3=(x+y)\cdot (x^2-xy+y^2)=u\cdot (u^2-2v-v)=u\cdot (u^2-3v) [/m]
[m]\left\{\begin{matrix}
v\cdot (u^2-2v)=\frac{10}{9}u^2\\v\cdot u\cdot (u^2-3v)=\frac{2}{3}u^3 \end{matrix}\right.[/m]
[m]\left\{\begin{matrix}
\frac{10}{9}u^2- u^2\cdot v+2v^2=0\\\frac{2}{3}u^2 - u^2\cdot v-3v^2=0 \end{matrix}\right.[/m] или [m]\left\{\begin{matrix}
v=0\\ u=0 \end{matrix}\right.[/m]
[m]\left\{\begin{matrix}
10u^2- 9u^2\cdot v+18v^2=0\\2u^2 - 3u^2\cdot v-9v^2=0 \end{matrix}\right.[/m]