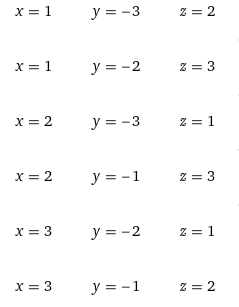Задача 55173 Решить систему уравнений ...
Условие
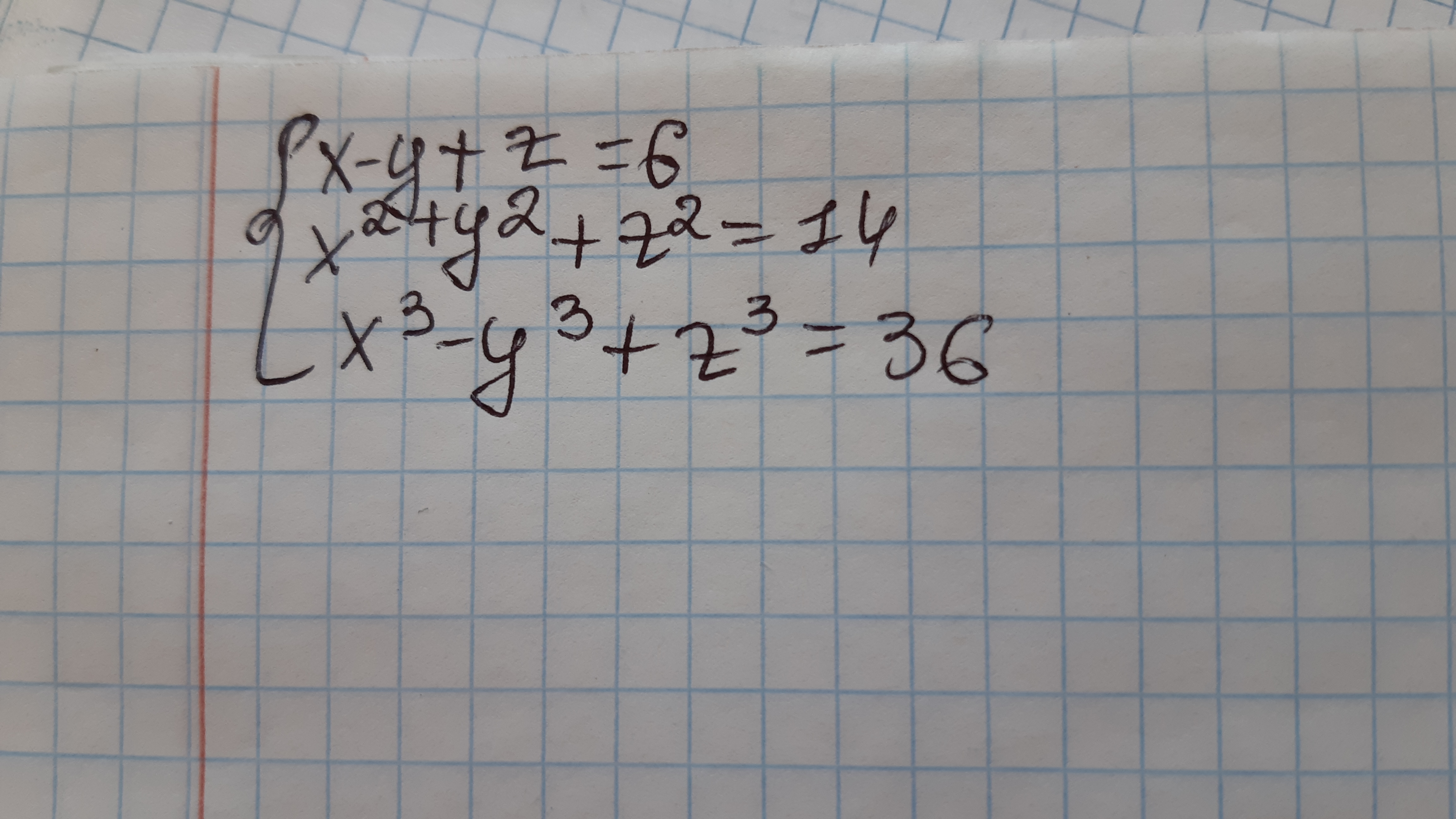
Решение
[m]\left\{\begin{matrix}z=6-(x-y)\\(6-(x-y))^2+(x^2+y^2)=14\\(6-(x-y))^3+(x^3-y^3)=36 \end{matrix}\right.[/m]
[m]\left\{\begin{matrix}z=6-(x-y)\\36-12(x-y)+(x-y)^2+(x^2+y^2)=14\\216-108(x-y)+18(x-y)^2-(x-y)^3+(x^3-y^3)=36 \end{matrix}\right.[/m]
[m]\left\{\begin{matrix}z=6-(x-y)\\36-12(x-y)+(x-y)^2+(x-y)^2+2xy=14\\216-108(x-y)+18(x-y)^2+(x-y)(x^2+xy+y^2)-(x-y)\cdot (x-y)^2=36 \end{matrix}\right.[/m]
[m]\left\{\begin{matrix}z=6-(x-y)\\36-12(x-y)+2(x-y)^2+2xy=14\\180-108(x-y)+18(x-y)^2+(x-y)\cdot (x^2+xy+y^2-(x-y)^2)=0 \end{matrix}\right.[/m]
[m]\left\{\begin{matrix}z=6-(x-y)\\11-6(x-y)+(x-y)^2+xy=0\\180-108(x-y)+18(x-y)^2+(x-y)\cdot 3xy =0 \end{matrix}\right.[/m]
Замена:
[m]x-y=u[/m]
[m]xy=v[/m]
О т в е т. 6 решений