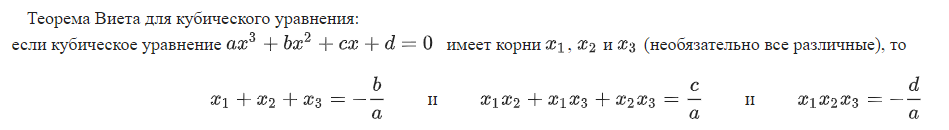Задача 55152 Решить систему уравнений { 1/x + 1/y +...
Условие
{ 1/x + 1/y + 1/z = 3
{ 1/xy + 1/yz + 1/zx = 3
{ 1/xyz = 1
математика ВУЗ
807
Решение
★
[b]xyz=1[/b]
умножаем на первое уравнение
[m] xyz\cdot (\frac{1}{x}+\frac{1}{y}+\frac{1}{z})=3[/m]
умножаем на второе
[m] xyz\cdot (\frac{1}{xy}+\frac{1}{yz}+\frac{1}{xz})=3[/m]
Получим систему
[m]\left\{\begin{matrix} yz+xz+xy=3
\\z+x+y=3\\xyz=1 \end{matrix}\right.[/m]
Это теорема Виета для кубического уравнения
t^3-3t^2+3t-1=0
(t-1)^3=0
t_(1)=t_(2)=t_(3)=1
⇒ x=y=z=1