Задача 55115 Постройте график функции...
Условие
Постройте график функции y=(x+4)(x^2+3x+2)/x+1 и определите, при каких значениях m прямая y = m не имеет с графиком ни одной общей точки.
Решение
Функция [m] y=\frac{(x+4)(x2+3x+2)}{x+1} [/m] определена при всех х, кроме х=-1 ( на ноль нельзя делить)
[m] y=\frac{(x+4)(x+1)(x+2)}{x+1} [/m]
Но если сократить на (x+1), то получим другую функцию:
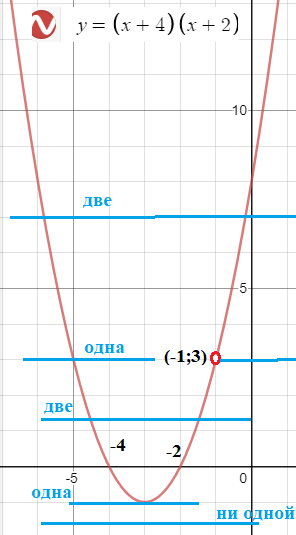
[m]y=(x+4)(x+2)[/m] - это квадратичная функция она определена при любых х, графиком является парабола.
Две функции совпадают во всех точках точках, кроме одной, у которой x=-1
Значит, графиком [m] y=\frac{(x+4)(x2+3x+2)}{x+1} [/m] является парабола [m]y=(x+4)(x+2)[/m]
с "выколотой " точкой , абсцисса которой х=-1
По графику видно, что вторая координата этой точки y=3
Прямая y=m - прямая, параллельная оси Ох
По рисунку видно, что такие прямые могут пересекать параболу в двух точках, в одной точке и вообще не пересекать
Не пересекают при m ∈ (- ∞ ; -1)
Но гораздо чаще спрашивают именно про одну точку пересечения.
Таких прямых две: это y=-1 и y=3