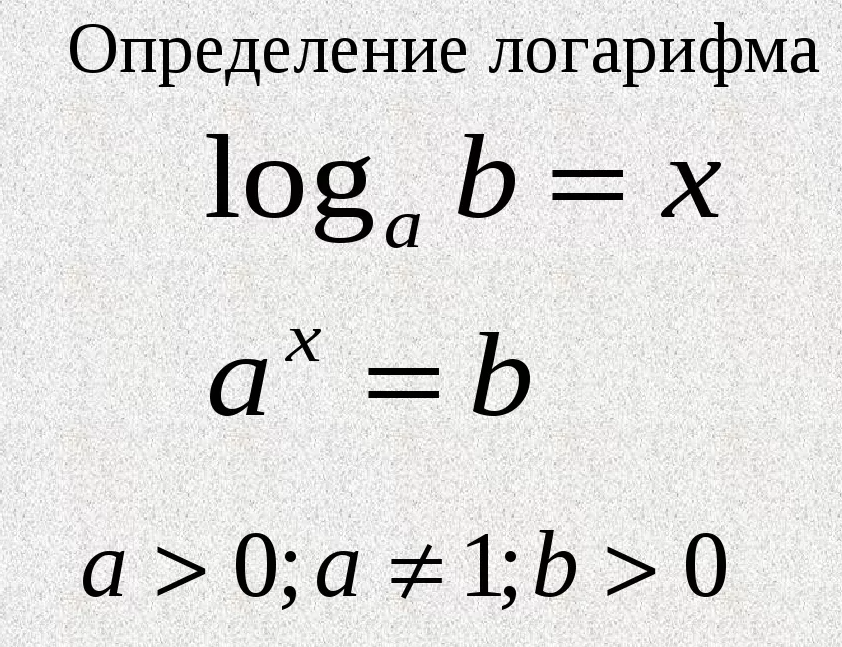Задача 55103 решите уравнения log_(x)...
Условие
log_(x) (8x-15)=2
log_(x+2) (3x^(2)-12)=2
математика 10-11 класс
785
Решение
★
8x-15=x^2
x^2-8x+15=0
x>0; x ≠ 1 ( основание логарифмической функции не может быть отрицательным и не может равняться 1)
Под знаком логарифма не может быть отрицательного выражения, но раз уж x>0, то автоматически получаем, что 8x-15 =x^2 >0)
D=64-4*15=4
[b]x=3; x=5[/b]
3x^2-12=(x+2)^2
x+2 >0
x+2 ≠ 1
3x^2-12=x^2+4x+4
2x^2-4x-16=0
x^2-2x-8=0
D=4+32=36
x=-2 или [b] x=4[/b]
x=-2 - не является корнем, так как не удовлетворяет условию: x+2 >0