Задача 55079 ...
Условие
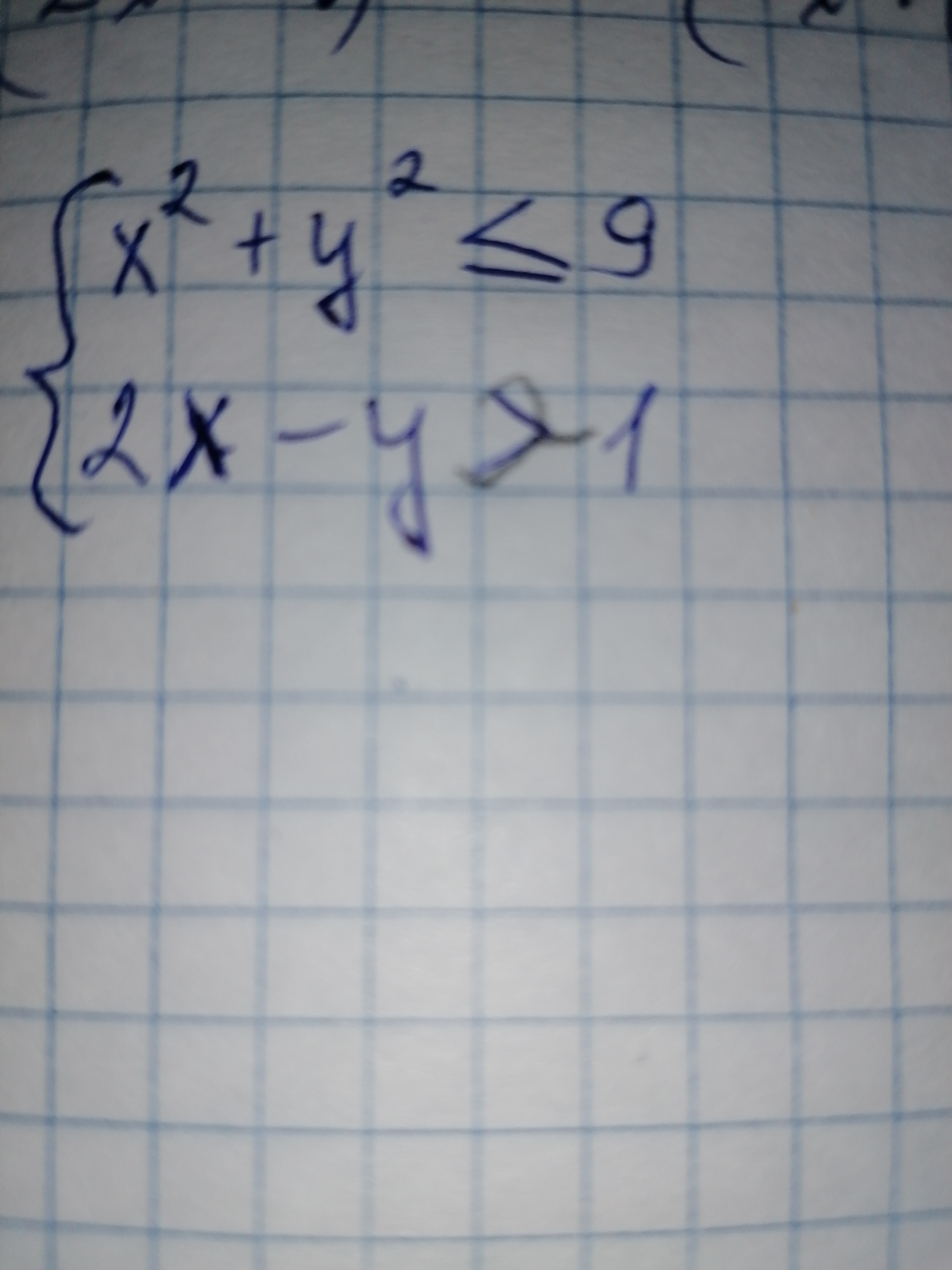
Решение
x^2+y^2 ≤ 9\\ 2x-y > 1\end{matrix}\right.[/m]
[b]Первое неравенство:[/b]
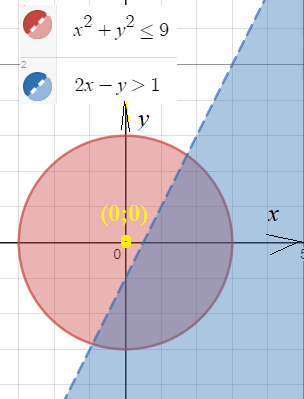
[m]x^2+y^2 ≤ 9 [/m] - внутренность круга с границей
Границей является окружность с центром (0;0) радиусом 3
На рис. область красного цвета
[b] Второе неравенство:[/b]
[m]2x-y > 1[/m]
[m]2x-y-1 >0 [/m] - область синего цвета без границы
Граница - прямая [m]2x-y-1=0 [/m] ⇒ [m]y=2x-1 [/m] , строим по точкам (0;-1) и (2;3)
Прямая разбивает плоскость на две части. Неравенству удовлетворяет область справа от прямой.
Как узнать? Взять любую точку из этой области, например,(0;0) и подставить её координаты
в неравенство: [m]2\cdot 0 -0 >1 [/m]
[m]0 >1 [/m] - неверно.
⇒ Значит область, содержащая точку (0;0) не удовлетворяет неравенству,
а область, не содержащая точку (0;0) - есть ответ.
Системе:
[m]\left\{\begin{matrix}
x^2+y^2 ≤ 9\\2x-y > 1\end{matrix}\right.[/m]
удовлетворяет пересечение областей.
О т в е т.