Задача 54969 ...
Условие
Решение
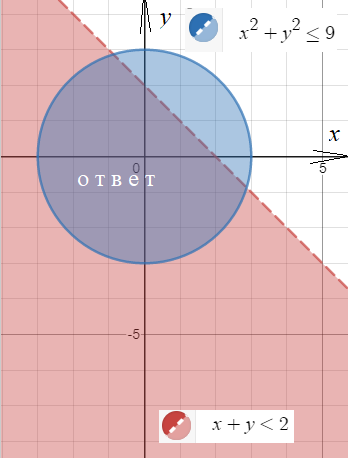
[m]x +y<2 [/m] - задает на плоскости область красного цвета без границы ( изображена пунктиром, потому что неравенство строгое)
Граница [m]x +y=2 [/m] - прямая, строим по точкам (1;1) и (2;0)
Прямая разбивает плоскость на две части. Неравенству удовлетворяет область слева от прямой.
Как узнать? Взять любую точку из этой области, например,(0;0) и подставить её координаты
в неравенство: [m]0+0<2 [/m] - верно.
⇒ Значит область, содержащая точку (0;0) удовлетворяет неравенству,
[b]Второе неравенство:[/b]
на плоскости задаёт внутренность круга вместе (неравенство [b]нестрогое[/b]) [i]с окружностью[/i]:
[m]x^2+y^2=9[/m]- центр в точке (0;0), радиус 3