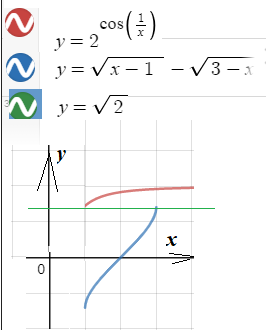Задача 54789 Как решить неравенство...

5f54df62356816184059ff63

21.10.2020 17:43:10

Как решить неравенство sqrt(x-1)-sqrt(3-x) больше или равно 2^(cos1/x)

5f3ea7e3faf909182968ddd9

21.10.2020 18:28:30

★

ОДЗ:
{x-1 ≥ 0 ⇒ x ≥ 1
{3-x ≥ 0 ⇒ x ≤ 3

x ∈ [1;3] ⇒
y=√(x–1) - возрастает на ОДЗ
y=√(3–x) - убывает на ОДЗ ⇒ y=-√3–x - возрастает на ОДЗ

y=√(x–1)–√(3–x) = √(x–1)+(-√(3–x)) [i] возрастает[/i] на ОДЗ как сумма возрастающих функций

Причем

[b]- √2[/b] ≤ √x–1–√3–x ≤ [b]√2[/b]


[b]1 ≤ x ≤ 3[/b]

[b]y=1/x[/b] - [i]убывающая[/i] функция на [1;3], тогда

(1/3) ≤ (1/x) ≤ 1

[b]y=cost [/b] - [i]убывающая[/i] функция на [1/3;1], тогда

cos 1 ≤ cos (1/x) ≤ cos(1/3)

[b]y=2^(z)[/b] - [i]возрастающая[/i] функция на [cos 1 ; cos(1/3)], тогда

[b]2^(cos1) ≤ 2^(cos(1/x)) ≤ 2^(cos(1/3))[/b]

2^(cos(1/x)) > 2^(cos1) при всех [b]1 ≤ x ≤ 3[/b]

[i]Осталось сравнить[/i]

2^(cos1) и sqrt(2)=2^(1/2)

1 рад < ( π/3) ⇒ cos1 > cos(π/3) =1/2

Поэтому

2^(cos1) > 2 ^(1/2) на [1;3]

О т в е т. ни при каких х