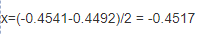Задача 54467 Отделить корни уравнения 2^x - 5х - 3=0 ...
Условие
Решение
2^(x)=5x+3
и решим его графически:
Построим графики функций: y=2^(x) и y=5x+3
-1 < x_(1)<0; 4 < x_(2) < 5
Теперь картина понятна, как решать задачу аналитически
Рассматриваем данное уравнение.
Пусть
f(x)=2^(x)-5x-3
f(-1) =2^(-1)-5*(-1)-3=2,5 >0
f(0)=-3
на концах [-1;0] функция f(x) принимает значения разных знаков,
значит один корень уравнения принадлежит отрезку [-1;0]
Делим этот отрезок пополам
Рассматриваем два отрезка [-1;-0,5] и [-0,5;1]
f(-0,5)=2^(-0,5)-5*(-0,5)-3=(1/sqrt(2))-0,5 >0
Значит, на концах отрезка [-0,5;0] функция f(x) принимает значения разных знаков,
корень уравнения принадлежит отрезку [-0,5;0]
Делим этот отрезок пополам.
Рассматриваем два отрезка [-0,5;-0,25] и [-0,25;0]
f(-0,25)=2^(-0,25)-5*(-0,25)-3<0
значит, на концах отрезка [-0,5;-0,25] функция f(x) принимает значения разных знаков,
корень уравнения принадлежит отрезку [-0,5;-0,25]
Делим этот отрезок пополам.
и так далее