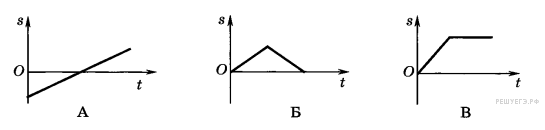
Задача 544 На каком из графиков изображена...
Условие
1) А
2) Б
3) В
4) Такой график отсутствует
физика 10-11 класс
13429
Решение
Ответ: 3
1) А
2) Б
3) В
4) Такой график отсутствует

Ответ: 3