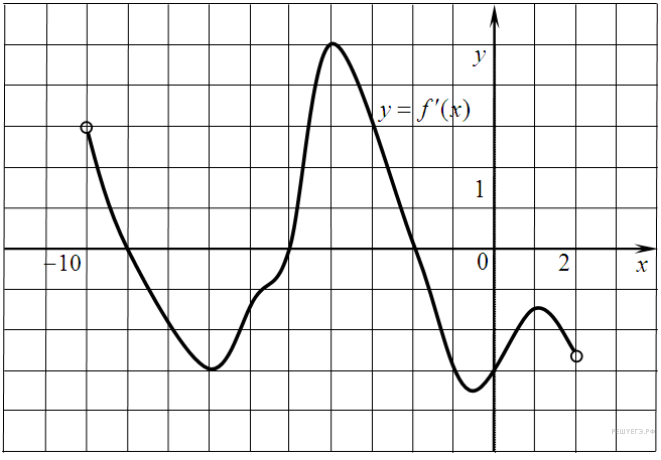
На рисунке изображен график производной функции f(x), определенной на интервале (-10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = -2x-11 или совпадает с ней.
математика 10-11 класс
17855
Значение производной в точке касания равно угловому коэффициенту касательной. По-скольку касательная параллельна прямой y = -2x-11 или совпадает с ней, их угловые коэффициенты равны –2. Найдем количество точек, в которых y'(x0) = -2, геометрически это соответствует количеству точек пересечения графика производной с прямой y = -2. На данном интервале таких точек 5.
Ответ: 5

