Задача 53911 Самостоятельная работа Изобразите на...
Условие
Изобразите на координатной плоскости множество точек, заданное системой неравенств
Уровень А
1) [m]\begin{cases}
y > x^2 + 1 \\
2x \leq 1 - y
\end{cases}[/m]
2) [m]\begin{cases}
y^2 + x^2 \geq 4 \\
x^2 + y^2 < 16
\end{cases}[/m]
Решение
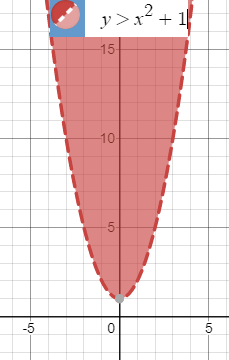
Граница первой области- парабола y=x^2+1
Изображаем пунктирной линией, так как неравенство строгое.
Это линия разделила плоскость на две части
Проверяем какая из них удовлетворяет неравенству.
Выбираем любую точку, например, точку (0;0)
Подставляем ее координаты в неравенство:
0>0^2+1 - неверно
Значит, неравенству удовлетворяет область, в которой не лежит точка (0;0)
Это внутренняя часть параболы.
2 x=1-y ⇒ y=1-2x
Это граница второй области. Прямая.
Для ее построения достаточно найти две точки
Например, x=1; тогда y=1-2*1=-1
(1;-1)
x=3; y=1-2*3=-5
(3:-5)
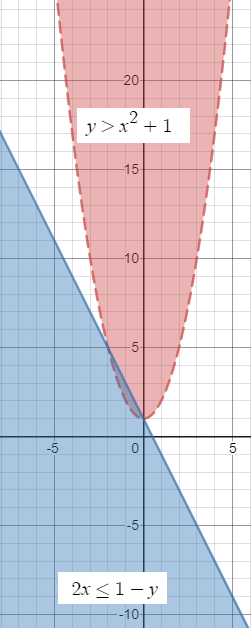
Прямая разбивает область на две части.
Выбираем точку, (0;0)
2*0 ≤ 1-0 -верно
Синяя область, содержащая точку (0;0) удовлетворяет второму неравенству.
Системе удовлетворяет пересечение областей.
см. рис. 2 ( область сине-красного цвета)
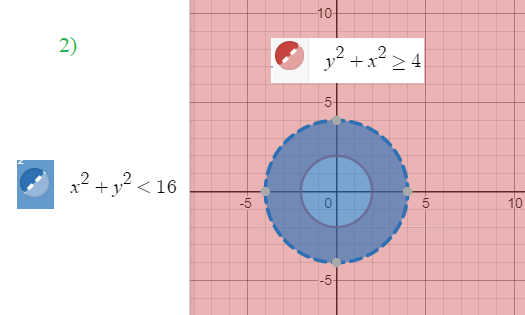
2) y^2+x^2 ≥ 2 внешность круга радиуса 2 с границей
x^2+y^2<16 - внутренность круга радиуса 4 без окружности
Система удовлетворяет кольцо между окружностями