Задача 53891 ...

5f72a4be5e684a139991de2b

5 октября 2020 г. в 18:48

Решите систему неравенств графически:
a)

{ 2x + y ≤ 3
{ y ≥ x² + 2

b)

{ y – x < 4
{ x² + (y + 1)² ≤ 25

c)

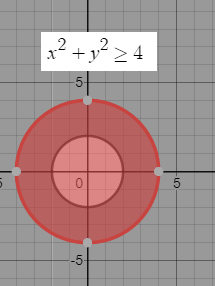
{ x² + y² ≥ 4
{ x² + y² ≤ 16

5f3ea7e3faf909182968ddd9

5 октября 2020 г. в 18:57

★

1.

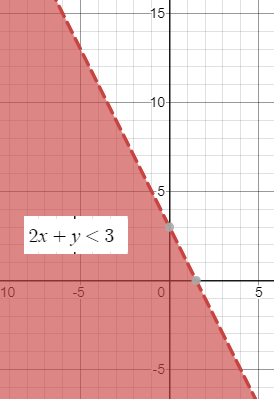
2x+y=3 – граница первой области, прямая.
Изображаем пунктирной линией, так как неравенство строгое
Эта прямая разбивает плоскость на две части.
Точка (0;0) например, удовлетворяет неравенству,
2·0+0 < 3 – верно

Значит неравенству удовлетворяет та часть плоскости на рис.1, которая содержит точку (0;0)

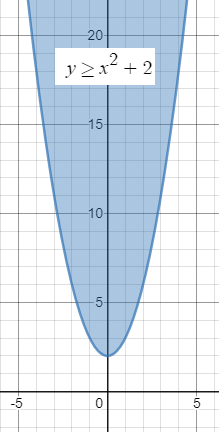
y=x²+2 – граница второй области, парабола, сплошной линий, неравенство нестрогое.

Точка (0;0) не удовлетворяет неравенству y ≥ x²+2
Значит неравенству удовлетворяет внутренняя часть параболы.
(рис.2)

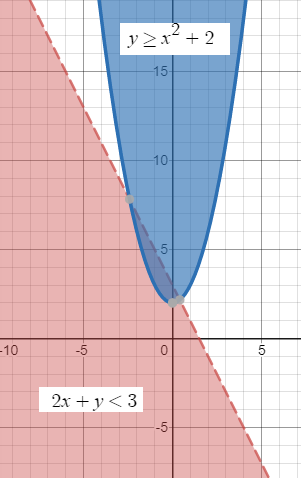
Системе неравенств удовлетворяет пересечение областей на рис. 3

это часть внутренней области параболы, красного цвета.

2.
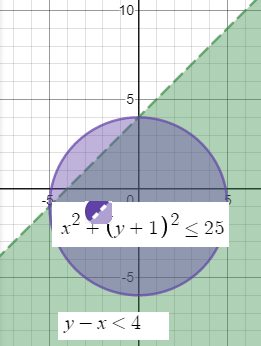
x²+(y+1)² ≤ 25 – внутренняя часть круга с центром (0;–1), R=5

Cистеме неравенств удовлетворяет
эта часть в пересечении с зеленой областью, рис. 4

3.
x²+y² ≥ 4 –внешняя часть круга с центром (0;0); R=2
x²+y² ≤ 16 – внутренняя часть круга с центром (0;0), R=4
Cистеме неравенств удовлетворяет кольцо серо–красного цвета